郭强 周孝信
中国电力科学研究院,100085 北京清河
1 引言
灵活交流输电系统(FACTS)技术是现代电力技术发展的一个重要方向,它可以提高电力系统的传输能力和稳定性水平。可控串联电容器(TCSC)作为FACTS元件的一种,其电抗值可以在一定范围内快速连续地变化,因而与传统的固定式串联补偿电容相比,不但可以用来补偿线路电抗提高传输能力,还可以用于抑制低频振荡和次同步谐振,提高系统的静态和暂态稳定性。目前,国外已有一些TCSC装置投入或即将投入运行。例如,美国已有3套230~500 kV的TCSC装置投入运行,用于控制潮流、提高输电能力和阻尼振荡。我国东北的伊敏电厂—冯屯—大庆500 kV输电线路原来也计划装设TCSC,以提高传输能力,减少一回出线[1],由于某些原因,这一工程目前已推迟。
TCSC在提高系统稳定性、抑制振荡方面的作用已得到公认,人们在如何设计TCSC的控制器以充分发挥其作用方面也进行了许多研究。文献[2]对TCSC用于抑制地区间振荡进行了研究,并以特征值分析为基础设计了控制方法。文献[3]采用线性输出反馈的方法设计了TCSC的控制规律,用以提高系统的动态性能。文献[2][3]均采用了在运行点附近局部线性化的数学模型,因此它们不能很好地适应运行方式的变化,对提高暂态稳定性的控制效果也受到影响。近年来,人们对非线性控制理论在电力系统中的应用进行了大量研究。例如,文献[4]提出单机无穷大系统TCSC非线性变结构控制,文献[5]提出TCSC非线性预测自调控制。这些研究结果表明,采用非线性控制理论和方法可以克服线性方法的一些缺点。
文献[6][7]提出了可控串补非线性自抗扰控制,这种控制方法不依赖于被控系统模型,适应性较好。但其参数选取工作量很大,需要进行大量的仿真试验才能获得较为满意的结果。为此,本文应用优化方法来选取参数,使参数选取的工作得以自动进行,从而减轻了工作量。
2 基本原理
可控串补非线性自抗扰控制的原理如下[7]:
系统输出为
y=∫t0(Pe-Pe0)dt (1)
扩张状态观测器为
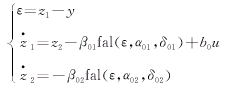 (2) (2)
积分串联型输入为
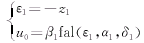 (3) (3)
可控串补等值电抗为
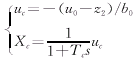 (4) (4)
其中
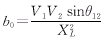 (5) (5)
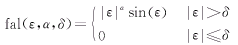 (6) (6)
在上面公式中 V1、V2和θ12分别为装设可控串补线路两端的电压幅值和相位差;XL为线路电抗;uc为可控串补底层控制的输入;Xc为可控串补的等值电抗。
从以上的控制方法可见,非线性自抗扰控制的参数较多,通过仿真试验选取合适的参数的工作量较大。为此,采用优化方法来自动地选取控制参数,以减少工作量。
参数优化问题可以描述为
min J(u)=∫Tt0|ωa-ωb|eαtdt
式中 u={u1,u2,…,un}为需要优化的参数;ωa和ωb为最大相对摇摆角所对应的一对机组的角速度;α为大于0的常数;(t0,T)为暂态过程经历时间。
显然,用这一目标来确定控制参数,系统在可控串补的控制下,将会使发电机转子间的相对角速度得以减小,从而最大限度地取得提高暂态稳定性的效果。
为了求解这一优化问题,需先求得目标函数对参数的梯度,而这一优化问题包含了系统的暂态过程,要准确地求得其梯度是比较困难的。为此,可以采用差商来近似地代替偏导数,即
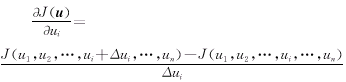 (7) (7)
式中 Δui为在第i个参数上施加的微小增量。
梯度为
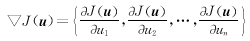
这样,就可以应用一些高效率的带导数优化算法来求解这一优化问题,例如BFGS算法。具体步骤如下
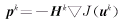 (8) (8)
uk+1=uk+αkpk (9)
式中 pk为第k步搜索方向;αk为第k步搜索步长;Hk为一正定矩阵,按照BFGS算法递推形成。
重复上面步骤直至收敛,即可得到优化参数。
3 仿真试验及结果
本文所提方法以东北伊敏电厂送出工程为例进行了仿真试验。东北系统简化为一8机系统,其接线如图1所示。伊敏电厂通过双回500 kV线路向东北主网输送大量电力,暂态稳定问题比较突出。为解决这一问题,计划在伊敏(10号节点)-冯屯(17号节点)线路冯屯侧装设可控串补。
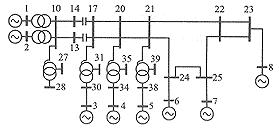
图1 东北系统简化接线图
Fig.1 Northeast power system diagram
为充分发挥可控串补提高系统稳定性、阻尼振荡的作用,对其采用非线性自抗扰控制,并用本文所提方法进行参数优化。在目标函数中,伊冯系统ωa及ωb分别取为伊敏电厂2号等值机和系统等值机(6号机)的角速度,α=0.2。根据各个参数对控制效果的影响,取u=(β01,β02,β1),并将其初值取为
β01=10 β02=100 β1=0.0012
其它参数取值如下:
α01=0.5 α02=0.5 α1=1.5 δ01=0
δ02=0.00005 δ1=0.005 Tc=0.03
所研究的故障情况为:0 s时,伊冯线冯屯侧发生三相短路故障,0.1 s切除故障线路。对伊冯系统不同的运行方式进行了参数优化。表1给出了优化结果。
表1 参数优化结果
Tab.1 Parameter optimization results
伊冯线
传输功率
优化参数
拟合参数
β01
β02
β1
β01
β02
β1
1380MW(1)
42.81
242.60
0.001158
42.81
242.60
0.001155
1480MW(2)
43.94
229.66
0.001155
44.16
221.20
0.001155
1580MW(3)
45.49
196.61
0.001155
45.51
199.80
0.001155
1640MW(4)
46.34
187.93
0.001155
46.34
187.93
0.001155
由优化参数可以看出,β1近似不变,而β01和β02与传输功率近似成线性关系。因而对于不同的运行方式,β1可以采用优化参数的平均值,β01和β02可由近似线性关系拟合而得到。表中拟合参数一栏给出了所得的各运行方式下的近似优化参3贫杂τ谠诵蟹绞?~4的优化参数为参数1~4。表2给出了各种运行方式和参数下的目标函数值。
表2 目标函数值
Tab.2 Objective function value
伊冯线
传输功率
目标函数
初值参数
参数1
参数2
参数3
参数4
拟合参数
1380MW
23.71
12.09
12.58
16.67
17.63
12.09
1480MW
29.12
11.58
10.98
14.98
16.06
11.73
1580MW
44.85
18.02
17.11
15.71
16.09
15.92
1640MW
82.15
47.34
24.54
22.18
21.16
21.16
图2给出了传输功率为1640 MW时的伊敏电厂2号机相对于系统等值机的摇摆曲线,图3给出了相应的可控串补等值电抗的变化情况。在图中,细线表示采用初值参数的情况,粗线表示采用拟合参数的情况。
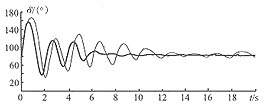
图2 Pe0=1640 MW时的摇摆曲线
Fig.2 Swing curve when Pe0=1640 MW
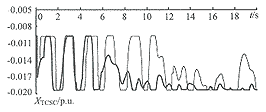
图3 Pe0=1640 MW时的可控串补等值电抗
Fig.3 Reactance of TCSC when Pe0=1640 MW
由表2和图2可以看出,应用优化方法选取控制参数可以有效地提高可控串补的控制效果。从表2还可以看出,采用拟合参数所得到的目标函数值与采用各自运行方式下的优化参数得到的目标函数值在多数情况下是比较接近的。这说明用近似线性拟合方法得到的不同运行方式下的优化参数是可行的。线性拟合是一种近似的简化方法,在某些情况下,其效果与优化参数相比有一定的差距(例如本例方式2),但与未经优化的初值参数相比,效果仍有较大提高。
4 结论
应用优化方法确定可控串补非线性自抗扰控制的参数,可以提高可控串补的控制效果。本文所提方法同非线性自抗扰控制的原理相结合,可得到比较完整的设计可控串补非线性自抗扰控制器的实用方法。以伊冯等值8机系统为例进行的仿真试验结果证明了所提方法的优越性。
|


