江振华1,程时杰1,傅予力2,廖晓昕2
1.华中理工大学电力工程系,湖北省武汉市430074;2.华中理工大学自控系,湖北省武汉市430074
1 引言
可控串联补偿电容(TCSC)作为灵活交流输电系统(FACTS)家族的一员,在改善电力系统性能方面具有很多优点,近年来引起电力工业界很多研究人员和工程技术人员的关注,其研究得到了迅猛的发展。将TCSC用于电力系统,能够控制系统潮流、改善系统的稳定性、提高功率传输极限。有些研究结果表明TCSC还具有抑制电力系统次同步谐振和阻尼电力系统振荡的效果。同时,以往发生的多起大电网中因机组轴系扭振引发的事故,曾引起电力界人士的广泛关注,很多研究人员深入研究了电力系统次同步谐振产生的机理和控制策略,取得了一定的成绩。但以往的研究常局限于常规交流输电系统最多是包含高压直流(HVDC)或静止无功补偿(SVC )等简单补偿设备的电力系统。随着FACTS设备的应用,分析它们对电力系统次同步谐振的影响以及寻求抑制次同步谐振的控制策略,已成为当前的迫切任务。
在前人工作的基础上,本文简要介绍用于分析次同步谐振的复数力矩系数法及其对系统各部件模型的要求的基础上,从TCSC的物理模型出发,建立了适用于复数力矩系数法分析次同步谐振的TCSC的数学模型,推导出TCSC的复频域等效端口导纳矩阵,编制了复频域扫描程序,利用所编制的程序对有用的结论。同时通过对该系统的全时域仿真验证了这些结论的正确性。
2 用于分析次同步谐振的复数力矩系数法
复数力矩系数法是由瑞士的I.M.Canay博士于1982年提出的。其基本思想是用2个复数力矩系数Ce(jλ)和Cm(jλ)分别表征次同步振荡时的脉动电磁力矩和动态机械力矩,然后根据这2个系数判断系统的稳定性。
当给系统中某一台发电机的相对角度δ施加频率为λ的小扰动Δδ时,包括网络、发电机等在内的电气系统和发电机机械系统分别产生复数电磁转矩响应ΔTe和复数机械转矩响应ΔTm,它们都是许多状态变量的函数。对6段集中质量弹簧系统轴系模型而言,只保留发电机转子质量段的转角增量Δδ,而把其它所有状态变量都看作中间变量进行消元,这样就可以将电磁转矩增量和机械转矩增量化为单一变量Δδ的函数,其系数为等效复数电磁力矩系数Ce(jλ)和等效复数机械力矩系数Cm(jλ),这2个复系数的虚部分别表示对于频率λ的等效电气阻尼系数De(λ)和机械力矩的等效机械阻尼系数Dm(λ)。定义复数电气转矩系数为
Ce(jλ)=ΔTe/Δδ=Ke+jλDe(1)
复数机械转矩系数为
Cm(jλ)=ΔTm/Δδ=Km+jλDm(2)
对全系统在0—50Hz内进行频率扫描,当在某个频率λ0满足
Ke(jλ0)+Km(jλ0)=0(3)
时,若出现
De(jλ0)+Dm(jλ0)<0(4)
则系统将在该模态(λ=λ0)因不稳定而发生次同步振荡[1]。
在含有FACTS设备的多机交直流系统中,可以采用分散消元方式的复数力矩系数法分析次同步振荡。首先推导出包括FACTS在内的电力系统各种元件的复频域模型,其次结合交直流联合系统的复频域网络方程,消去中间变量,得出全系统相对于被研究发电机组的复频域等效端口导纳矩阵,最后可求出全系统在被研究发电机组的等效电气阻尼特性(关于分散消元方式的复数力矩系数法及常规电力系统元件的复频域模型,可参阅文[1])。
3 TCSC的数学模型
图1为TCSCa相电路结构图。它由一对并联晶闸管控制的电感和电容器并联而成。由于晶闸管的开关性能,整个电路的动态特性包括连续特性(电容电压)和离散事件(晶闸管触发),为了建立TCSC的连续数学模型,必须考虑晶闸管触发对电容电压的影响[2-4]。
 图1 TCSC单相结构框图
图1 TCSC单相结构框图
对于稳态运行的电力系统,假设线路电流IL保持为正弦波形,晶闸管的触发角保持不变,当晶闸管完全导通时,TCSC相当于一个并联的LC回路,其方程为

当晶闸管完全关断时,TCSC相当于一个串联的电容器,其方程为

写成矩阵形式
y=PBIdq0(8)
式中 y=V,P=[1 0]。
为不失一般性,假设当前运行时刻为k且位于晶闸管的截止时段内,晶闸管下一触发时刻为Φ1/2,晶闸管相应的关断时刻为τ1/2,半个周期后运行时刻为k+1/2,随着运行时刻的推移,相应时刻分别为Φ1、τ1、k+1、…。据此可画出线路电流和电感电流波形以及触发时刻,如图2所示。
假设在时刻k的电容电压为V(k),由于在每半个周期内晶闸管导通和关断1次,所以在时间间 隔[k,Φ1/2]内对方程(8)积分,在[Φ1/2,τ1/2]内对方程(6)积分,在[τ1/2,k+1/2]内对方程(8)积分,从 而可预测在时刻(k+1/2)的电容电压V(k+1/2)。
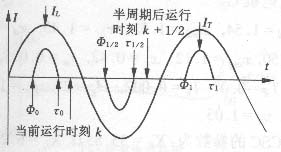 图2 TCSC的波形和触发时刻图
图2 TCSC的波形和触发时刻图
 (13)
(13)
式(9)~(13)表明,某一时刻的电容电压V(k+1/2)是半个周期前的电容电压V(k)、此前半个周期内线路电流Idq0(k)和触发时刻τ1/2、Φ1/2的函数,将其在运行点附近线性化并整理后可得(考虑到ΔΦ=0)

对于一稳定运行的系统,b、c相电流和触发相角分别滞后于a相120°和240°,从而可相应得出b、c相的方程。将a、b、c三相方程合写成如下矩阵形式
△Vabc(k+1/2)=Mabc△Vabc(k)+Nabc△Idp0(k)
(17)
式中 ΔVabc(k)=[ΔVa(k),ΔVb(k),ΔVc(k)]T,ΔIabc(k)=[ΔIa(k),ΔIb(k),ΔIc(k)]T,Mabc=MI,I为三阶单位阵,Nabc=diag(Na,Nb,Nc)。
式(17)就是TCSC在采样频率为T/2(T为网络线电流的周期)时的离散系统方程。为了与电力系统其它元件和网络方程统一建模,应将上述电容电压从abc坐标系转换到dq0坐标系。经派克变换,得出在dq0坐标系下的TCSC离散系统模型
△Vabc(k+1/2)=Mdp0△Vdp0(k)+Ndp0△Idp0(k)

为了求得TCSC的连续时域模型,构造其解为式(18)的连续微分方程为

当ΔT较小时,此误差很小。
由于数据采样周期很小,每工频周期有3个采样点,因而该模型在0至50 Hz范围内是有效的。
4 TCSC的复频域等效端口导纳矩阵
式(19)给出了TCSC在坐标系dq0下的连续模型,考虑到对称运行电力系统的0轴分量为零,只须考虑dq轴分量,则可得到TCSC在坐标系dq下的电压电流关系式为
Vdq=K′vVdq+K′iIdq(21)
式中 Vdq=[ΔVd,ΔVq]T,Idq=[ΔId,ΔIq]T。
由于网络复频域方程以网络坐标系xy为基准,所以将TCSC模型接入网络模型之前,应该将坐标系dq下的方程转化到坐标系xy(如图3所示)。
设q轴滞后y轴的角度为θ,定义

则存在变换
Vdq=R(θ)Vxy,Idq=R(θ)Ixy。
从而,式(21)转化为
R(θ)Vxy=K′vR(θ)Vxy+K′iR(θ)Ixy(22)
对上式作Laplace变换,得
sR(θ)Vxy(s)=K′vR(θ)Vxy(s)+K′iR(θ)Ixy(s)(23)
即
[sR(θ)-K′vR(θ)]Vxy(s)=K′iR(θ)Ixy(s) (24)
由于Ixy(s)=YTCSC(s)Vxy(s),从而TCSC的复频域等效端口导纳矩阵为
YTCSC(s)=[R(θ)]-1(K′i)-1(sI2×2-K′v)R(θ) (25)
上式即为表示TCSC的复频域等效端口导纳矩阵。相应地,TCSC可用图4所示的框图来表示。

图4 TCSC的复频域模型
5 计算实例
为了用所提方法分析TCSC对电力系统次同步谐振的影响,下面就1个2机5节点系统采用复频域扫描程序进行分析计算。
5.1 系统及其参数
一具有5个节点的2机电力系统及其参数设置如图5所示。额定频率为50 Hz,发电机及其励磁系统的参数(标么值表示)为发电机G1
xd=1.79,xmd=1.66,xfd=1.7,x′d=0.169,xq=1.71,xmq=1.58,x′q=0.228,ra=0.006,Ka=50.0,Ta=0.01,Te=0.002,Hg=25,pg=0.95,qg=0.78,Vg=1.05
发电机G2
xd=1.54,xmd=1.32,xfd=1.43,x′d=0.23,xq=1.50,xmq=1.12,x′q=0.42,ra=0.005,Ka=50.0,Ta=0.01,Te=0.002,Hg=25,pg=1.0,qg=0.8,vg=1.05
TCSC的参数为:XC=35.85Ω,XL=6.25Ω。
 图5 测试系统电路图
图5 测试系统电路图
5.2 计算结果及其分析
以发电机G1为研究对象,在几种不同的运行情况下使用复频域扫描程序,得出0~50 Hz区间电气阻尼的波形,分别如图6(a)~6(f)所示。通过仿真分析,可得出以下几点结论:
(1)比较图6(a),6(c)和6(d),可以看出TCSC距发电机越近,它对该发电机次同步谐振的影响越明显。这是因为TCSC距离发电机越近,在仿真计算时,TCSC的加入对等效网络的导纳矩阵影响越大。
(2)从图6(b)、6(c)和6(d)可以看出,固定串联电容补偿比TCSC补偿的系统更易发生次同步谐振。由于TCSC的触发角可以控制,其补偿阻抗可调,因而实际运行时[1] [2] 下一页
|


