曹 路,李海峰,陈 珩,曹 然
东南大学电气工程系,江苏省南京市210096
1 引言
可控串联补偿装置(TCSC)是一种重要的灵活交流输电系统(FACTS)设备,可以起到调节潮流、抑制振荡、减小短路电流、提高系统稳定性等作用,尤其适用于远距离高压输电系统。由于TCSC中加入了电力电子器件,在进行仿真研究时需要作特殊处理。
TCSC的研究模型可分为功能模型和器件模型。功能模型把TCSC作为理想的可变电抗支路,通常用一阶惯性环节模拟TCSC对命令电抗的响应过程。器件模型则模拟TCSC的实际结构,包括电容器、并联电感、反并联晶闸管等器件。在仿真过程中,通过晶闸管的导通和关断实现TCSC的阻抗改变。由于器件模型能最大程度地保持TCSC的真实结构,因此器件级仿真可以反映出TCSC的实际动作以及系统对TCSC实际动作的响应。
本文以东北电网伊敏-大庆可控串补输电工程为例[1],采用西门子公司提供的NETOMAC软件对TCSC器件模型进行了数字仿真研究。
2 TCSC器件模型
2.1 模型及参数
TCSC的器件模型如图1所示。其中:
·电容器C的电容值为119.2μF,基波容抗为26.7Ω;
·并联电感L的基波感抗为4.5Ω,计及晶闸管管压降,并联电感回路的总品质因数Q为50;
·金属氧化物可变电阻MOV作为非线性电阻,用V-A特性表示,见表1,保护水平为2.2倍。TCSC等效电抗的可调范围在-5.6Ω(感性)至80.1Ω(容性)之间。
考虑到三相晶闸管并非同时导通,需要对三相分别建模,分别触发。
图1 TCSC器件模型


2.2 触发过程
在晶闸管关断状态下,TCSC相当于普通串补。当晶闸管承受正向电压,且门极有触发信号时,晶闸管导通,并联电感支路有电流流过,TCSC等效阻抗将改变。触发信号出现的时刻(或称触发角α)与TCSC等效基波阻抗Xc之间有如下对应关系[2]:

根据式(1)和上列参数,可用曲线表示出Xc与α角的关系,如图2所示。图中,Xc数值为正表示TCSC呈容性,反之为感性。触发角在90°处为旁路状态,180°处为闭锁状态,在143°附近为谐振区,运行时应避开,以免产生谐振,危及设备。
实际研究中,可事先将Xc与α的对应关系以表格形式表示,由Xc快速查出触发角α,用于触发控制。

2.3 触发控制
TCSC触发控制是指控制TCSC中晶闸管触发信号出现的时刻,使TCSC的等效阻抗能平滑快速地跟踪命令阻抗,以发挥TCSC的控制作用。
研究表明,在容性区域内,晶闸管导通时间越长,并联电感支路电流越大,电容电压uc中的谐波分量也越大。为此采用了快速富里叶(FFT)算法,滤出线路电流il和uc的基波分量,进而根据阻抗的定义,得到TCSC的等效基波阻抗。
如果采用简单的开环控制,则调节时间和超调量受命令电抗Xord的影响较大,调节效果不理想。所谓命令电抗就是由控制策略要求的电抗。为了能使TCSC对不同的命令电抗都有较好的响应,在触发控制中采用了具有在线参数调整的不完全比例积分微分(PID)控制器,如图3所示。

图3 具有在线参数调整的不完全微分
PID控制器原理框图
对不同的命令电抗,分别用开环控制器和具有在线参数调整的不完全微分PID控制器进行TCSC触发控制,得到的响应曲线见图4。命令电抗为53.4Ω时,TCSC的电压和电流响应波形见图5。
由图4可见,具有在线参数调整的不完全微分PID控制器对不同命令电抗都有较好的控制效果。而图5显示,在晶闸管导通前,电容电压uc、线路电流il、电容电流ic均保持正弦;触发后,电感支路在晶闸管导通期间出现电流iTCR,使电容电流、电容电压中出现谐波分量,而线路电流的变化不明显。这些现象是用功能模型仿真时无法获得的。
2.4 仿真步长的选择
在进行TCSC器件级仿真时,需要选择较小的步长。这是因为,TCSC中的每个反并联晶闸管在一个基波电压周期内正负向各导通一次,三相反并联晶闸管在一个周期内需要触发6次。对于50 Hz系统,相当于3.33 ms触发一次,所以仿真步长必须小于3.33 ms方可确保晶闸管能正确触发。
但是,为得到正确的TCSC等效阻抗,步长还应减小,因为等效阻抗与晶闸管的触发角度直接相关。根据图2,在谐振区两侧,等效阻抗的变化比较剧烈,触发角改变很小便使等效阻抗变化很大。为保证等效阻抗的跟踪效果,仿真步长需要足够小。但另一方面,小的仿真步长会引起计算耗时的延长,也将带来累积误差,影响计算精度。所以在进行TCSC器件级仿真时,选择合适的步长是非常重要的。
图6显示用不同的仿真步长得到的TCSC等效阻抗的阶跃和斜坡响应。可见,不同的仿真步长会产生不同的结果。步长取1ms时,等效阻抗的响应很差,不能有效地跟踪命令电抗的改变;随着步长的减小,阻抗响应逐渐好转,至0.05ms和0.1ms步长时,等效阻抗与命令电抗很接近,跟踪速度也较快,表明这样的仿真步长较为理想。考虑到0.05ms和0.1ms步长的阻抗响应相当接近,为减少计算耗时,可取仿真步长为0.1ms。

图4 TCSC对
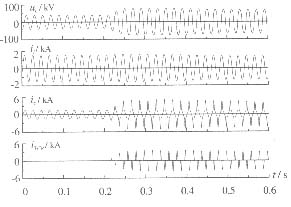
图5 TCSC的电压和电流在触发过程中的波形(A相)

图6 仿真步长对等效阻抗响应的影响
3 工程实例
伊敏电厂位于内蒙古东部,为坑口电厂,一期工程装机2×500MW,二期工程装机2×600MW,所发电力通过500kV线路经冯屯、大庆变电站送往东北电网,主要供给辽宁地区负荷。由于出线困难,伊敏至大庆只允许架设双回线路。而该线路又长达487km,为提高系统的暂态稳定性,决定在冯屯变电站装设TCSC。研究中所用的等值系统如图7所示,由17台发电机(包括等值机)组成,含140个节点、120条支路、69台变压器、42个负荷以及主要机组的调节系统。

研究中采用模糊逻辑控制方法作为TCSC的暂态稳定控制器,TCSC的模型分别采用图1所示器件模型和以一阶惯性环节表示的功能模型,惯性时间常数取为0.03s。仿真中采用的故障型式包括三相短路和单相接地短路。三相短路过程为:TCSC线路侧在0.1s发生三相短路,经0.1s断路器将故障线路切除。单相接地短路过程为:TCSC线路侧在0.1 sA相接地短路,经0.1s故障相被切除,经0.8sA相重合,故障仍然存在,又经0.1s故障线路三相切除。
在故障期间,为防止MOV的能耗过高,将TC-SC转入旁路状态,即由电容转为小电感。故障清除后的2s内,TCSC又变回容性,且将在工作能力的允许范围内把串补度调节至最大,以充分发挥其作用。在由感性转换到容性的过程中,插入了持续时间为一个周期的晶闸管闭锁状态,使TCSC进入容性区后能正确触发。
根据以上条件,用NETOMAC软件进行数字仿真计算,可得暂态稳定过程中伊敏厂的发电机功角摇摆曲线,如图8所示。可见,采用器件模型和功能模型的仿真结果基本一致,说明二者在系统中的功能相同,也说明所采用的器件模型是正确的。

图8 伊敏厂的发电机功角摇摆曲线
TCSC的工作能力取决于线路电流[3]。线路电流大,则TCSC的等效电抗限制值Xlimit小,反之Xlimit大。图9给出了暂态稳定过程中电抗限制值Xlimit、命令电抗Xord和实际等效电抗Xact的变化曲线。可见模糊逻辑控制器输出的Xord均小于Xlimit,TCSC的触发控制也有较好的跟踪性能,保证了TCSC暂态稳定控制功能的实现。
图10显示了暂态过程中MOV的动作情况。在uc峰值超过128,228kV时,MOV电流imov将逐渐大,且符合表1中的V-A关系。

4 结束语
以上的研究表明,本文采用的TCSC器件模型可以适用于实际多机电力系统的数字仿真研究,选用的仿真步长和触发控制能够较好地体现TCSC的阻抗变化功能,并且能正确反映TCSC的电压、电流在触发过程中的实际波形,从而为进一步研究TC-SC设备的控制打下了良好的基础。
|


