任顺平 迟建平 庄洪春 刘来存
中国科学院空间科学与应用研究中心,北京,100080
1 引言
雷电的所有重要辐射过程包含于亚微妙场中[1~4],这种亚微妙场对电力网的正常运行、卫星上的星载仪器、飞机的导航设备及地面的通信、控制设备具有极强的破坏作用[5,6]。人们一直注意雷电精细结构的研究,但是,研究气体放电发现:气体放电的精细结构和高频噪声很像微观混沌现象,其微观描述是非常困难的,对雷电的微观刻画也有同样的结论[7]。为了提高电网、通信系统及各种星载设备的抗电磁干扰能力,在研究微观物理机制的基础上建立雷电电磁辐射场的宏观模型是仿真雷电亚微妙场的重要方法。
分形学是混沌现象的有力几何工具,分形技术已经成功地描述气体放电路径[8]。气体放电的物理机理与雷电的原理基本是一致的,有理由相信气体放电的主要结论完全可以应用于雷电。从工程应用角度,而不是严格的数学证明,直接假定闪电具有分形特征,将真实的雷电物理参数代入到分形中去,会取得良好的雷电描述结果。实际上,在以往的闪电路径和其电磁辐射场中,已经隐含了分形的思想。Lin等人于1980年提出了将闪电等效为垂直于大地的直导线,大地为平坦的无穷大导体的雷电模型[9]。该模型成功地解释了在Florida雷电回击的电磁辐射场的测量结果[10,11]。Le Vine等人于1978年利用Lin模型,假设闪道中回击电流的传播速度为光速,闪道由一端一段的直线组成,给出了雷电回击的麦克斯韦方程组精确解[12]。文献[12]中探讨的局部线形闪道的思想就是分形技术的萌芽。本文从分形概念出发,借鉴Le Vine辐射场的运算方法,利用中点置换法形成分形闪道,计算雷电回击辐射场,计算该闪道辐射场的分形维数,找出闪道形状与辐射场的内在联系,为分形雷电回击辐射场的仿真提供了一条捷径。
2 分形闪道的生成方法
分形闪道的生成是对工程精度而言的。作为数学上的分形具有无限精细的自相似结构。工程上,只要满足一定精度,即可认为是分形的。本文假定闪道由N段方向任意、长短以一定概率分布的直线组成。生成这样一种弯曲的具有分形特点的闪道常采用中点置换法[13]。
设空间闪道上的任意一点为r=rc表示为空间高度的函数:
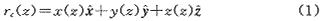
式中x(z)和y(z)表示空间水平面的两个垂直坐标,它们是以z为自变量的分形曲线;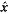 、 、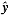 、 、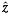 分别为空间坐标x、y、z方向的单位矢量。 分别为空间坐标x、y、z方向的单位矢量。
为了简化,设定x(z)和y(z)为具有相同概率分布、相同分形维数的独立随机变量。在此,仅就x(z)的分形生成阐述分形闪道的生成方法。
中点置换法是借助布朗运行的增量具有相似性来实现分形闪道的。设随机过程B(t)为布朗运行,则该过程有如下两个性质:
(1)增量B(t2)-B(t1)服从高斯分布;
(2)均方增量正比于时间的变化。即
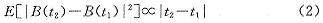
B的增量具有统计自相似。即B(t0-t)-B(t0)及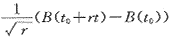 对 对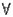 t0及r>0有相同的有限维数。 t0及r>0有相同的有限维数。
不相关高斯白噪声W的积分就是满足上述性质的布朗运行。即
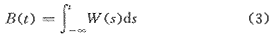
此处的随机过程W(t)是不相关的,并服从正态分布N(0,1)。由此产生的布朗运动的分形维数为1.5。
更一般分形维数闪道的生成,选取分形布朗运动,B(t)满足下式
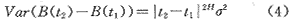
生成的分形闪道的分形维数为
D=2-H (5)
文献[13]对该方法有详细阐述。
3 分形闪道的辐射场的精确解[12]
考虑一段长为l,任意方向处于空间,单位方向为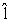 的闪道,则通过闪道的电流为 的闪道,则通过闪道的电流为
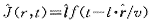
式中v为电流沿闪道传播的速度;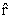 为闪道上某点r的空间矢量。 为闪道上某点r的空间矢量。
假设闪道的方向任意,大地为无穷大的平面导体,电流在闪道中以光速传播,则可推得频域电磁场为
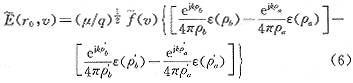
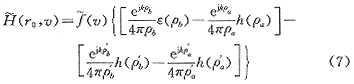
式中下标a、b代表直线的始点和末点,肩上有撇的符号代表镜像电磁场的量,带有波浪号的符号代表原量的傅立叶变换。
值得注意的是,镜像源的坐标、单位方向与源坐标和闪道的单位矢量的关系。设rs为空间闪道上任意点的矢量坐标,为其单位方向矢量,镜像源对应的变量为:
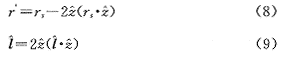
设定i为a或b,则式(6)(7)中的其他量分别为
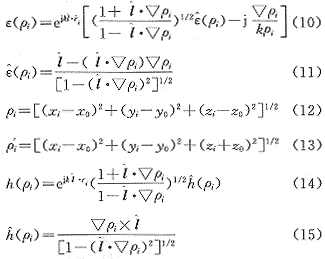
式中 r0为观测点坐标。
在时域中,其电磁场的精确解为:
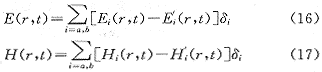
式中 对i=a或i=b分别有δa=-1,δb=1。
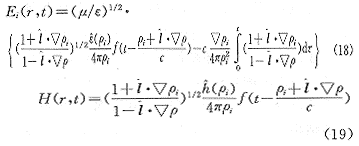
在这里,镜像场不再赘述,只要将源场的许多相应量换成镜像响应量即可。
式(6)是仅针对一般直线而言的电磁辐射场。如果有多段相连的导线或闪道,只要将其辐射场在观测点矢量累加即可。
4 分形维数的计算
分形维数的求取一般采用数盒法(box-counting method),如图1所示,将被考查的曲线所在平面按统一尺度,沿两个垂直方向归一化,选取一定的分割间隔rI,将平面分成小方盒,数出曲线坐落于小方盒的个数NI,曲线的分形维数D为
ln(Ni)=-D.ln(ri)+c (20)
式中c为方盒形状因子。
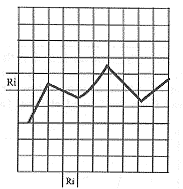
图1分形维数方盒分割示意图
Fig.1 Schematic drawing of box-count method
针对不同的分割间隔会有不同的分形维数值,如图2最终的分形维数D的估值有2种方法,其一是选ln(Ni)-ln(r)平面中比较平直部分中的D值;其二是利用最小平方差估值,对ln(Ni)-ln(r)平面中的曲线进行一阶最小方差估计D。
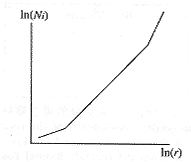
图2 分形维数确定范围示意图
Fig.2 The available range of the fractal dimension
分形维数计算中如果不能正确地处理一些问题,则得到的分形维数将不能反映真实的物理意义。这些问题是:
(1)方盒长度的选取
对于有限像素或有限点描述的实际曲线,分割长度太小,将导致计算的分形维数减小,极限为1[14]。文献[14]给出了最小分割长度rmin:
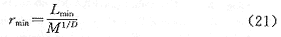
式中 Lmin为信号长度;M是总采样数;D是信号分形维数。
最小分割长度的选取是一个迭代的过程,选定rmin后,计算分形维数D,再根据式(21)计算最小分割长度。方盒的长度不能无限制的增大,文献[15]增加了一个新参数,即互相关系数来确定方盒最大边长rmax,rmax选取范围为rmin+1到M,rmax太大,则求取D的值根本不反映实际的分形维数。实际中,rmax每增加1时,计算此时的分形维数,并求它与最小平方差估计的分形维数的互相关系数,当互相关系数下降到一定值后,rmax不再增加,即可认为其已达到最大。
(2)统一量纲
在实际波形中,波形曲线的量纲并不是一样的。一般横轴为时间,纵轴为物理量(电压、电流、速度等),一定要从物理意义出发,统一两坐标的量纲。本文显示的分形闪道的电磁辐射场的横轴是时间、纵轴是电场,在距离的基础上统一起来,效果与实际波形基本一致。
(3)视窗的选择
在实际波形中,波形的每一部分的复杂程度不同,人们关心的对象也不同。因此,在考察对象中正确地选择视窗是非常重要的。本文重点考察从辐射场到达至延迟50μs的时间区域。在该区域基本反映了闪道弯曲对辐射的影响。
5 仿真结果
利用式(21)和假定流经闪道的电流以光速传播,闪道高度为6000m,同时,选用闪道回击电流为
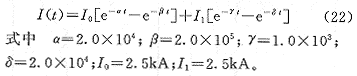
图3是流经闪道的电流波形。图4是直线闪道,在x-z、y-z平面的闪道图形,图5是闪道为直线时,距离100km处仿真的z方向电场辐射场。可以发现:在考察时间区域内,垂直电场波形变化不复杂;图6是利用1.2维布朗运行生成分形闪道在x-z、y-z平面闪道的曲线,闪道的真实维数为1.197±0.03。图7为距闪电落地点100km处(100,0,0)的仿真闪电回击辐射场的垂直电场分量,其波形分形维数为1.19±0.04。图8是与图6和图7同样闪道,在距闪电落地点10km处(10,0,0)的闪电回击辐射场的垂直电场分量,波形的分形维数为1.192±0.03。笔者同时仿真了闪道分形维数为1.5的电磁辐射场。由于仿真闪道与实际闪电形状根本不同,故没有给出图形,不过,仍然可以得出其电磁辐射场的分形维数与闪道的分形维数基本一致的结论。
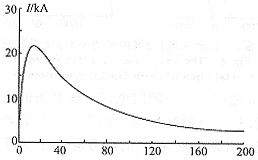
图3 沿闪道的电流波形
Fig.3The current wave from used to
generate examples of electric field
图4 垂直闪道x-z、y-z平面图
Fig.4 The (x,z) and (y,z)projections
of the vertical channel
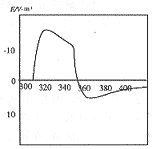
图5 垂直闪道100km处回击垂直辐射电场
Fig.5 The vertical component of the
return stroke radiated electric field at
ground level,r=100km away from the vertical channel foot
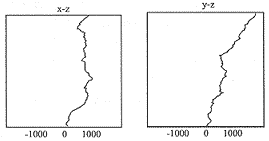
图6 分形生成1.2维闪道的x-z、y-z平面图
Fig.6 The (x,z) and (y,z)projections of
the fractal channel,with fractal
dimension D=1.2
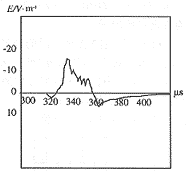
图7 1.2维闪道在100km处的垂直辐射电场
Fig.7 The vertical component of the return s [1] [2] 下一页
|


