任顺平 迟建平 庄洪春 刘来存
中科院空间科学与应用研究中心,100080 北京
1 引言
雷电和绝缘体击穿放电对人类许多活动如航天器的安全发射、电子通信、控制设备和计算机等精密设备的正常工作都有较大的影响。研究雷电和绝缘体放电击穿始终面临着微观放电机理与宏观电弧和雷电运动描述的关系问题。
绝缘气体、液体和固体的击穿现象非常复杂,常呈现树状和狭窄的随机放电通道,日常中的雷电也是这种结构[1~3]。该结构都有一个明显的特征即自相似结构,分形学正是描述该结构的最好工具[4]。本文试图将微观放电机理与其宏观特征用分形理论联系起来。
最简单的绝缘气体击穿放电模式是理想的二维辐射放电,在2mm厚玻璃夹层内加0.3MPa的SF6气体、棒极加正高压脉冲电压30kV×1μs,板极接地[5]。放电图形如图1所示。该图为Lichtenberg图的一种。L.Niemeyer等人对此图进行了详细分析[6],根据B.Mandelbrot提出的分形维数的概念,得到半径r内和半径上的放电通道分岔数与半径r和分形维数D的关系为
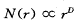
(1)
式(1)亦可改为N(r)的微分形式,即
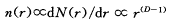
(2)
 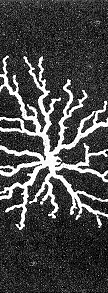 
图1 实际放电图片
Fig.1 The photograph of a surface leader discharge
经过仔细数分岔数,得到图1的分维数约为1.7。
为了研究绝缘放电的特性,L.Niemeyer等人提出了格点式随机模型,并在计算机上给予仿真,该方法被称为DBM。DBM的主要算法如图2所示,具体步骤如下:
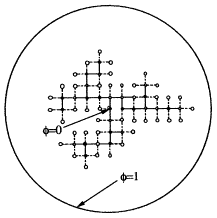
图2 DBM方法示意图
Fig.2 Illustration of DBM model
①图2给出运行几步的放电仿真,已放电点用黑点表示,放电点间用黑粗线连接;新的可能放电点用白圈表示,新的可能放电点与已放电点用细虚线连接,新的可能放电点间无联线。图中每一格点的电位由离散Laplace方程求取,边界条件为放电点的电位φ=0,圆外点的电位φ=1;
②每一步放电过程是:在已放电格点周围存在的未放电格点都是新的可能放电点,图2用白圈表示,与已放电点用细虚线连接;
③ 这些新的可能放电点的放电可能概率p正比于其局部场强,因为击穿点(i,j黑格点)的电位φij=0,可能击穿点(i′,j′白圈)的电位φi′j′击穿概率为

(3)
其中η为功率指数, φi′j′满足Laplace方程
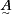
(4)
Laplace方程的离散形式为
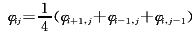
(5)
以此模型仿真绝缘体击穿现象取得了很好的结果,当η=1,运行5000步的仿真结果如图3所示。分形维数D=1.75±0.02;表1列出了L.Niemeyer等人的工作, 随功率指数η的不同,分形维数D的变化。
表1 分形维数D与功率指数η的关系
η
0
0.5
1.0
2.0
D
2
1.89±0.01
1.75±0.02
~1.60

图3 当η=1时,5000步仿真结果
Fig.3 Example of computer-generated discharge
pattern of about η=1 and 5000 steps
2 简单模糊集合仿真方法
DBM虽然取得了很好的仿真效果,但也有不可克服的缺陷:①在DBM中,某点的可能击穿概率是由该点电场强度求得,该点是否击穿完全按此概率计算。实际上,局部场强低于某值时,该点根本不可能放电;②许多实验结果、理想参数和先验知识加不到仿真之中,更重要的是人们仿真的目的是建立模型、找出机理、预测未来,为此常常忽略模型次要部分,抓住主要影响因素,DBM是随机模型不可能简化。
模糊数学[7]同分形学一样,是一门新兴的学科。如果说分形学能够最真切地描述客观世界,那么,模糊数学则是最好表达人类思想的工具。模糊数学能够自然合理地将先验知识、参数和人的想法加入到事物的处理和描述之中。
模糊事件是客观存在的,不以人的意志而转移。它不是概率事件,只是难以确切地说清而已。在强电场下,绝缘材料的空间击穿场强本身就是一个模糊值。对于具体某一材料的某点而言,确实存在着击穿值,不是随机的。由于人们认识的局限性,不可能给出材料的每点击穿场强。经验表明,电场强度大到一定程度时才可能发生击穿现象;同时,电场强度小到一定程度时会使放电停止。为此,建立以相对场强为度量的可能击穿点模糊集合。设模糊集合的论域U,它包含所有可能击穿点,即图2中的白圈点,记为
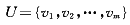
(6)
其中vi为仿真中可能击穿点,其坐标为(k,n),为某一白圈点。
设可能击穿点模糊集为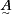 合,记为 合,记为
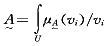
(7)
式中 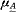 (vi)为模糊集合 (vi)为模糊集合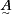 的隶属函数。 的隶属函数。
根据绝缘击穿的经验,取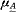 (vi)的值为某可能击穿点的电位(或称电场强度)φk,n与可能击穿点中最大电位(电场强度)φM的比值,即 (vi)的值为某可能击穿点的电位(或称电场强度)φk,n与可能击穿点中最大电位(电场强度)φM的比值,即
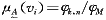
(8)
模糊集合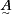 反映了论域U中每个元素击穿可能性大小的经验评价。该模糊集合通过λ截集转化普通集合 反映了论域U中每个元素击穿可能性大小的经验评价。该模糊集合通过λ截集转化普通集合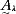 ,其定义为 ,其定义为
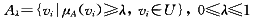
(9)
Aλ是论域U上的普通集合,是由模糊集合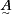 的隶属函数大于或等于λ的元素组成的集合Aλ。更确切地说,可能击穿点中电场强度大到一定程度的点才属于集合Aλ。在以后的讨论中,只有集合Aλ中的元素才可能被击穿。 的隶属函数大于或等于λ的元素组成的集合Aλ。更确切地说,可能击穿点中电场强度大到一定程度的点才属于集合Aλ。在以后的讨论中,只有集合Aλ中的元素才可能被击穿。
有了模糊集合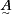 和普通集合Aλ及以上讨论的思想,就可以实现简单模糊分形仿真绝缘材料平面放电的算法,具体步骤如下: 和普通集合Aλ及以上讨论的思想,就可以实现简单模糊分形仿真绝缘材料平面放电的算法,具体步骤如下:
(1)按式(6)、(7)和(8)构造模糊集合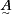 ,选定阈值λ,经式(9)确定可能放电元素vi。注意,该放电元素不再是论域U的全部,只是它的一部分。 ,选定阈值λ,经式(9)确定可能放电元素vi。注意,该放电元素不再是论域U的全部,只是它的一部分。
(2)将集合Aλ中的元素按DBM的方法进行仿真。
3 仿真结果及说明
图4为η=1,λ=0,仿真500步形成的分形图形,按式(1)求得分形维数D=1.77±0.02;图5为η=1,λ=0.1,仿真450步形成的分形图形,求得分形维数D=1.74±0.02;图6为η=1,λ=0.2,仿真400步形成的分形图形,求得分形维数D=1.71±0.02;图7为η=1,λ=0.3,仿真350步形成的分形图形,求得分形维数D=1.68±0.02;图8为η=1,λ=0.4,仿真300步形成的分形图形,求得分形维数D=1.64±0.02;图9为η=1,λ=0.5,仿真250步形成的分形图形,求得分形维数D=1.55±0.03;图10为η=1,λ=0.6,仿真200步形成的分形图形,求得分形维数D=1.44±0.03。注意:仿真步数的选择是为防止放电通道延伸到仿真画面之外。

图4 η=1,λ=0仿真图

图5 η=1,λ=0.1仿真图

图6 η=1,λ=0.2仿真图
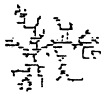
图7 η=1,λ=0.3仿真图

图8 η=1,λ=0.4仿真图
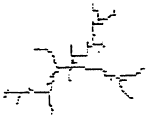
图9 η=1,λ=0.5仿真图
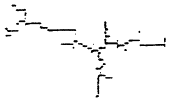
图10 η=1,λ=0.6仿真图
由图4可见,虽然仿真条件与L.Niemeyer等人的一致,但由于仿真步数较小,电场强度差异也小,每步放电机会基本均等,所以仿真图形的分形维数较大;从图4~7可见,随λ增加,分形维数不断下降,当λ=0.2或0.3时,分形维数基本与实际相符;图8、9和10的分形维数下降很大,它们的分岔数和复杂程度大大减弱,只留下平面放电的几个主干道。
4 结论及展望
本文阐述的模糊分形描述平面气体放电的方法是DBM模型的改进。将人们的观测和实验的先验知识变成隶属函数,虽然具有很强的主观性,但在处理方法上是一个进步。从仿真结果可见,DBM模型按概率仿真的平面放电分形维数为1.75左右,如果以等概率在平面随机行走的话,形成图形的分形维数为2。
DBM方法中隐含了竞争机制,当有一点击穿后,平面格点的击穿概率就不再相同了,随着击穿的发展,击穿发展快的通道会越来越快。本文改进型方法不但保持了DBM方法的竞争机制,同时,合理地限制了实际中不可能击穿点,使仿真结果更接近实际。虽然该方法不是对所有的Lichtenberg图的仿真都适用,但是它为分形学用于其它平面放电图案的仿真提供了思路。
同时,该方法可为避雷针保护范围的运算提供借鉴。在考虑避雷针保护范围时,通常采用滚球法计算,其中的物理含义是等场强等受击概率,并没有考虑闪电是发展过来的,有其自身的惯性,亦未考虑最小能量及击穿阈值和停止击穿阈值。利用模糊理论加概率的方法,可能使避雷针保护范围的计算更精确。
该方法对国际上比较成熟的两种雷电模型的改进有借鉴意义。一种是研究雷电发展方向的模型。 [1] [2] 下一页
|


