赵中原1 邱毓昌1 马翠姣1 冯江2 袁检2 蔡庆3
1.西安交通大学 西安710049 2.国家电力公司武汉高压研究所 武汉430074 3.上海市东供电局 上海200122 4.泉州电力学校 泉州362000
0 引言
局部放电进行在线监测可发现绝缘早期故障。判断电气设备是否发生局部放电,常用“指纹”诊断法,即根据局部放电的放电量q、放电发生时的工频电压相位φ及每秒内的放电次数n来判断。本文提出了基于数学分形理论的提取局部放电特征量方法,实验与分析结果表明它描述局部放电特征的准确率较好。
1 分形理论及数学模型
1.1 分形理论
分形学是研究自然界中复杂和不规则事物的表现及其内在规律的一门新兴的科学。自80年代初,数学家Mandelbort提出了分形理论,用分形概念来描述自然形态和现象以来,该理论已发展应用于科学和技术的很多领域。在研究具有“自相似性”、“自仿射性”的对象时,分维特征是用于识别的十分有效的特征[2]。
1.2 数学模型
分数布朗运动(FBM)为一常用分形数学模型,其定义如下:
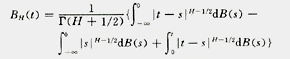
式中H ∈(0,1),B(t)为一般的布朗运动函数。FBM是描述具有统计自相似、时间长程相关、功率谱满足指数规律的非平稳随机过程的数学模型之一。它是一个非平稳的高斯过程,具有以下关系:
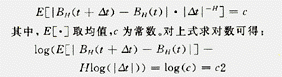
利用最小乘法可求得H值,分维值D=DT+1-H,其中DT为拓扑维[3]。
理论分析及实测表明,电机、GIS的局部放电脉冲的上升沿很陡(ns级),脉宽也仅为几个到几十个ns,放电脉冲可用高斯分布函数近似。因其分布为非平稳高斯[4],可用FBM描述局部放电过程 。设曲线上某一点x对应的信号幅度为f(x),则有:
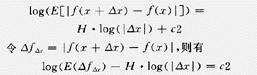
其中:Δx=1,2,3,…,m
用最小二乘法拟合数据点对{log(E(ΔfΔx)),log(|Δx|)}的拟合直线的斜率即为H值,由此可求得局放的分形维数D=2-H。分形模型拟合误差是FBM的另一参数,表征数据与分形模型的吻合程度,其公式为:
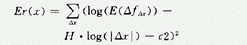
2 实验及其分析
为分析分形在局部放电特征提取中的应用,对1.5 cm空气间隙的棒—板电极逐渐施加电压,采集典型数据分析,取样速率1 GHz,图1为其中一组。
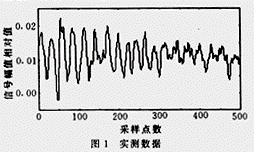
2.1 分形维数
施加电压U为0时,背景噪声的分形维数为1.1758。U=4.0、4.5 kV时,其分形维数分别为1.1571、1.0694。分形维数的变化规律表明背景噪声表现出较强的不规则性,其分形维数较高;而随着外施电压的逐渐增加,棒—板间发生放电现象且不断加强,从而增加信号的相似性,其分形维数逐渐减小。这与实际情况相符合,因而分形维数作为局部放电识别特征量是有一定效用的 。在强背景和随机噪声情况下,不同局放信号在分形维值上有可能相差无几[5],故须研究其它分维特征。本文提出用分维尺度变化量来描述局放的特征。
2.2 分维尺度变化量
理想分形体在所有尺度上均满足统计自相似性,分维数与尺度无关。但实际自相似性只体现在很小的尺度范围内,相应的分形维数在较小的尺度内才具有稳定性。所以,分形维数是随着尺度的改变而变化。下面计算信号在不同尺度下的分维值,研究其随着尺度变化的规律。对{log(E(ΔfΔx-1)),log(|Δx-1|)},{log(E(ΔfΔx)),log(|Δx|)},{log(E(ΔfΔx+1)),log(|Δx+1|)}作最小乘法拟合得到尺度Δx下的分维数D(Δx)如图2。可见尺度小时,分辨率高,能显露信号的细微变化,形成较强的不规则性,所以分维数较高。尺度大时则相反,分维数较低。U=4.5 kV时产生的局放增加了信号的自相似性,使其在较大范围尺度变化时,分维值变化缓慢。为表征这一特征,定义分维尺度变化:
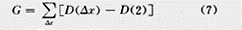

两个指标对局放程度的描述能力见表1。
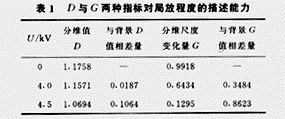
从表1中不难看出,分维尺度变化量比分维值具有更强的描述能力,前者具有更好的可分离性 。描述局部放电特征可获得较好的准确率。
3 结论
分维尺度变化量比分维值具有更强的描述能力,更好的可分离性,用于提取局部放电信号的特征是行之有效的。在没有信息冗余的情况下,将分维尺度变化量与其他特征量结合,将得到满意的结果。
参考文献
1 谈克雄等.基于人工神经网络的局部放电识别.高电压技术,1996,22(1):21
2 Falconer, Fractal Geometry Mathematical foundation and application New York: wiley, 1990
3 Lo T, Leugn H Fractal characterisation of seascattered signals and detection of seasuface target IEE Proc F Radio and Signal Processing, 1993, 140(4):243
4 周力行,李卫国.小波分析用于局部放电信号特征分析高电压技术,1999,25(2):15
5李新等.识别局部放电的新特征量——分维数的研究.高电压技术,2000,26(1):27
|


