刘明波 段晓军
华南理工大学电力学院, 510641 广州
1 引言
最优潮流问题(OPF)属于典型的具有可伸缩约束的多目标非线性规划问题。要对多目标问题寻求绝对最优解是相当困难的,有时甚至是不可能的。由于模糊集理论适合于描述不确定性以及处理不同量纲、相互冲突的多目标优化问题,所以模糊集理论在电力系统最优潮流中得到了广泛应用[1],为解决具有可伸缩约束的多目标优化问题提供了新途径。
文[2]对于无功优化问题,采用了线性规划结合模糊数学的寻优原理的综合处理方法,给出了各目标函数的最优隶属函数,使各个目标的令人满意程度达到最大,从而避免了寻求绝对最优解的困难。针对无功电压控制问题,文[3]采用模糊集将多目标函数和负荷电压模糊化,通过分段线性隶属函数,把原优化问题转化成标准的线性规划问题。新的目标函数表示了原来相互冲突的目标和可伸缩约束的折衷,通过线性规划算法求得最优解。文[4]采用潮流雅可比矩阵直接变换求取灵敏度系数矩阵,从而建立起无功电压控制的优化模型,其目标是系统网损最小。该文采用模糊集理论对已线性化的目标函数和无功控制的部分约束条件建模,把单目标线性规划问题转化为多目标模糊线性规划问题,其解空间是约束条件模糊集合与目标函数模糊集合的交集。文[5]把约束条件分为硬约束和软约束(可伸缩约束),然后利用模糊集把软约束和目标函数模糊化,得到模糊OPF问题,并采用线性规划法求解。文[2]~[5]的共同点是采用线性规划算法求解。近年来,有学者将原-对偶路径跟踪内点法应用于求解直接非线性OPF问题,在处理不等式约束以及迭代收敛性方面已显现出较明显的优势[6,7]。
本文利用模糊集理论将具有可伸缩约束的多目标最优潮流问题转化为单目标非线性规划问题,并采用直接非线性原-对偶路径跟踪法进行求解,试验系统优化计算结果表明,该算法具有许多优点。
2 多目标最优潮流问题的模糊化
对于一个由n个节点,l台发电机和k台无功补偿装置构成的电力系统,以有功网损和发电机总耗量为目标函数,节点电压具有可伸缩的约束,有功电源和无功电源的出力具有硬约束的多目标最优潮流问题可用下述形式的非线性规划模型描述:
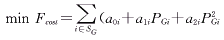 (1) (1)
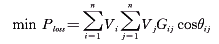 (2) (2)
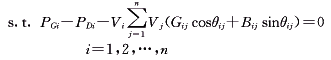 (3) (3)
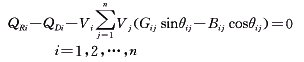 (4) (4)
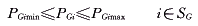 (5) (5)
QRimin≤QRi≤QRimax i∈SR (6)
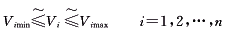 (7) (7)
式中 a0i,a1i,a2i为用二次多项式表示的耗量特性的零阶项、一阶项和二阶项的系数;PGi,QRi为节点的有功电源和无功电源的出力;PDi,QDi为节点的负荷的有功和无功功率;SG,SR为由l个发电机和l+k个无功电源构成的集合;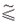 为模糊关系符,表示尽可能小,并且不会超过太多。 为模糊关系符,表示尽可能小,并且不会超过太多。
模糊化的关键在于隶属函数的确定。总希望在满足所有硬约束和最大限度地满足可伸缩性约束的条件下,目标函数越低越好,有上限而无下限。目标函数Fcost、Ploss及电压Vi的隶属函数分别可用以下的分段线性函数表示:
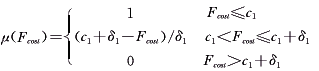 (8) (8)
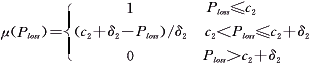 (9) (9)
 (10) (10)
式(8)中 c1+δ1表示发电机总耗量的最高可接受优化值,通常取优化前的数值,则其最小值就由所希望的最大节约量δ1决定。式(9)中有功网损的情况与之类似。式(10)中,当变量Vi超出故障极限Vimin和Vimax时,隶属函数则为零,表示不可接受;在正常极限Vimin+δvi和Vimax-δvi之间时,隶属函数则为1。
取一隶属变量λ为所有隶属函数中最小的,可称之为满意度:
λ=min{μ(Fcost),μ(Ploss),μ(V1),μ(V2),…,
μ(Vn)} (11)
则原多目标OPF模型可以转化为使满意度λ最大化的单目标非线性规划模型:
min -λ (12)
s.t. g(x)=0 (13)
Fcost+δ1λ≤c1+δ1 (14)
Ploss+δ2λ≤c2+δ2 (15)
-Vi+δviλ≤-Vimin i=1,2,…,n (16)
Vi+δviλ≤Vimax i=1,2,…,n (17)
xamin≤xa≤xamax (18)
0≤λ≤1 (19)
式中 xa为由有功电源和无功电源的出力构成的列矢量;x为由有功电源和无功电源的出力、节点电压幅值、节点电压相角(平衡节点除外,其电压相角为零)构成的列矢量;g(x)=0代表由式(3)和式(4)组成的潮流方程。
3 非线性原-对偶路径跟踪内点算法
将式(12)~(19)表示的非线性规划模型写成标准形式,并引入松驰变量,得
min a(x1,x2) (20)
s.t. g(x1,x2)=0 (21)
h(x1,x2)+sh=hu (22)
x1+su=xu (23)
x1-sl=xl (24)
sh≥0, su≥0, sl≥0 (25)
式中 x1为由xa和λ构成的列矢量,维数为2l+k+1;x2为节点电压幅值、节点电压相角(平衡节点除外)构成的列矢量,维数为2n+1;sh,su ,sl为由松弛变量构成的列矢量,维数分别为2n+2,2l+k+1,2l+k+1。
引入对数壁垒函数,将松弛变量的非负性约束消去,再对其等式约束引入拉格朗日乘子,得
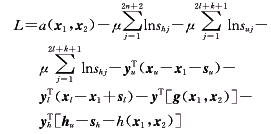 (26) (26)
式中 μ为壁垒参数,且μ>0;yh,yu,yl均为拉格朗日乘子矢量,且满足yh≥0,yu≥0,yl≤0,其维数分别为2n+2,2l+k+1,2l+k+1。
根据Kuhn-Tucker最优性条件可得
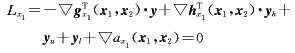 (27) (27)
 (28) (28)
Lsh=ShYhe1-μe1=0 (29)
Lsu=SuYue2-μe2=0 (30)
Lsl=SlYle3+μe3=0 (31)
Ly=-g(x1,x2)=0 (32)
Lyh=h(x1,x2)+sh-hu=0 (33)
Lyu=x1+su-xu=0 (34)
Lyl=x1-sl-xl=0 (35)
式中  gx1(x1,x2)、 gx1(x1,x2)、 gx2(x1,x2)分别为g(x1,x2)的雅可比矩阵的子矩阵; gx2(x1,x2)分别为g(x1,x2)的雅可比矩阵的子矩阵; hx1(x1,x2)、 hx1(x1,x2)、 hx2(x1,x2)分别为h(x1,x2)的雅可比矩阵的子矩阵; hx2(x1,x2)分别为h(x1,x2)的雅可比矩阵的子矩阵;  ax1(x1,x2)、 ax1(x1,x2)、 ax2(x1,x2)分别为a(x1,x2)的梯度的子矢量;Sh、Yh、Su、Yu、Sl、Yl为分别以sh、yh、su、yu、sl、yl的元素为对角元素的对角阵;e1、e2、e3均为单位列矢量,其维数分别为2n+2、 2l+k+1、 2l+k+1。 ax2(x1,x2)分别为a(x1,x2)的梯度的子矢量;Sh、Yh、Su、Yu、Sl、Yl为分别以sh、yh、su、yu、sl、yl的元素为对角元素的对角阵;e1、e2、e3均为单位列矢量,其维数分别为2n+2、 2l+k+1、 2l+k+1。
然后, 应用牛顿法求解由式(27)~(35)构成的非线性方程组,即可得Δx1、Δx2、Δy、Δsh、Δsu、Δsl、Δyh、Δyu、Δyl。其具体求解过程与文[6]类似。
因此,求解非线性多目标最优潮流问题的模糊优化算法的计算步骤可总结如下:
①输入模糊信息c1、δ1、c2、δ2、δvi,节点电压正常极限Vimin+δvi和Vimax-δvi,将多目标函数和部分可伸缩的约束条件模糊化;
②把多目标模糊最优潮流问题转化为式(20)~(25)形式的标准的单目标非线性规划问题;
③初始化 输入原始变量(包括松弛变量)和对偶变量(拉格朗日乘子)的初始值,并保证sh>0,su>0,sl>0,yh>0,yu>0,yl<0,0≤λ≤1;置收敛精度ε=10-6,给定合适的β(加速因子)值,β>1;
④计算补偿间隙gap=sTh.yh+sTu [1] [2] [3] 下一页
|


