鲁志伟1 史艳玲1 文习山2
1.东北电力学院电力工程系 吉林 132012 2.武汉大学电气学院 武汉 430072
0 引言
目前,有多种计算软件[1~3]可用来计算发变电站的接地电阻,但由于土壤电阻率的各向异性以及测量的误差,使计算结果与发变电站真实接地电阻值之间存在一定的差异。因此,有必要对接地系统的接地电阻进行现场实际测量。测量接地电阻普遍采用5D—0.618(D为接地网最大对角线的长度)直线法和2D—30°三角法。本文将分析这两种布极方法用于垂直分层土壤接地系统接地电阻测量所产生的误差,并提出可供工程实际测量参考的反向修正系数法。
1 均匀土壤中接地极接地电阻的测量误差分析
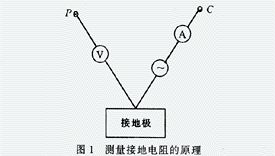
测量大型地网接地电阻,国内外均采用三极法。设电流极和电压极距接地极中心的距离分别为C和P,其引线间的夹角为β。由远离法可知,当C和P为无穷远时 ,采用图1的原理即可准确测量接地电阻。实际测量时,C和P均不可能离接地极无穷远,而当C和P移近接地极时,均产生测量误差。
设接地极为水平布置于地表面的圆盘半径为r,大地土壤电阻率为ρ,接地电阻为ρ/4r[4]。接地电阻的测量值R′为[5]:
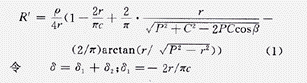
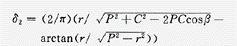
式中,δ为接地电阻的测量误差;δ1为C移近接地极产生的测量误差。由于C在接地极上产生负电位,使接地极电位下降,接地电阻测量值偏低,δ1总为负误差,δ2为P移近接地极产生的误差。若将P布置在零电位面,则δ2=0。将P由零电位面移近接地极,δ2为负值,这将使接地电阻测量值进一步降低。将P由零位面移近C,δ2为正值,使δ2=-δ1,此时由P产生的正误差补偿了由C产生的负误差,接地电阻测量误差δ为0,即补偿法。
例如,当β=0,C=5D=10r,P=0.618C则δ1=-6.3%,δ2=6.3%,δ=0;当β=30°,C=P=2D=4r时,δ1=-15.9%,δ2=14.7%,δ=-1.2%。所以P布极误差补偿了C布极误差。
2 垂直分层土壤中5D—0.618直线法的测量误差
如图2。设土壤垂直分层电阻率分别为ρ1,ρ2。圆盘接地极布置在ρ1区域,圆心距垂直分界面距离为2r,C和P布置在ρ1或ρ2区域,现对其测量误差分别探讨。

1)电流和电压引线不通过分界面
取平面直角坐标系。坐标原点与圆心重合,X轴垂直于土壤分界面,Y轴平行于土壤分界面。接地极和测试极及其镜象位置俯视图见图3。测试极引线同X轴夹角为α,图3中虚线位置为土壤分界面。
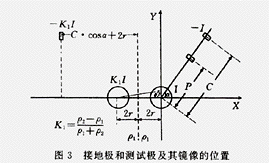
a) 圆盘接地极接地电阻的真值
采用平均电位法求镜象圆盘在接地极圆盘上产生的电位。在接地圆盘上任取一点,该点距圆心的距离为r1且与圆心的连线和负X轴夹角为θ,该点到

由曲面积分的基本原理,可求出镜象圆盘在接地圆盘上产生的平均电位U2为:
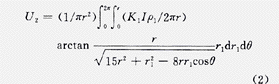
所以考虑镜象圆盘影响后,圆盘接地极电位U为:
U=(ρ1I/4r)+U2
对U2进行积分后可得圆盘接地电阻真值R0为:
R0=U/I=(ρ1/4r)(1+0.1623K1)
b) 接地电阻的测量值
参照图3,不难求出接地电阻的测量值R′为:
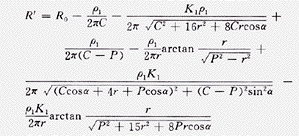
C和P移近造成的测量误差δ1和δ2分别为:

c) 计算结果及分析
表1给出了K1=-0.9~09,α=0°和90°时,5D—0.618直线法的测量误差。
由表1可见,若测试极不通过分界面,布置在任何方向上,5D—0.618直线法的测量精度均满足工程要求(相对误差绝对值<10%),且当测试极沿土壤分界面方向布置时,测量误差较小。

2) 电流引线和电压引线通过分界面
为讨论方便,设测试引线与分界面垂直,即布置在X轴负方向。计算ρ1接地极电位和ρ2电压极电位的镜象法原理见图4、5。
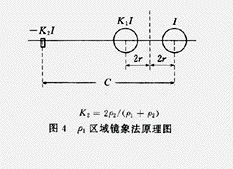 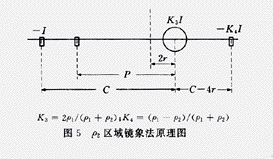
由图4、5可分别求得圆盘接地极的电位U1和P的电位Up,则接地电阻的测量值R′为:

表2给出了测试极引线通过分界面时,5D—0.618直线法在K1=-0.9~0.9测量误差。从表2可见,当测试极引线通过土壤垂直分界面,且是接地极位于低土壤电阻率侧,而测试极位于高土壤电阻率时,可能产生较大的误差。这主要是接地极和C之间的零电位面偏移造成的。以K1=0.7为例,与均匀土壤时相比,零电位面由0.5偏移到0.36,而此时的补偿点也由0.618偏移到0.42,如采用5D—0.618直线法,会产生较大的测量误差。

3 垂直分层土壤中2D—30°三角法的测量误差
设测试极引线通过垂直分层土壤分界面,C和P沿X轴负方向对称布置,即C引线和P引线与X轴负方向的夹角都是15°,略去推导过程,在C=P=4r的条件下得接地电阻测量值R′为:
&n [1] [2] 下一页
|


