刘树堂
东北电力学院建工系 吉林 132012
0 引言
拉门塔是送电线路中最为常用的直线塔型之一,具有受风荷小、用料少、安装组立方便等优点。它是由门型构架和构架平面外的拉线构成,二者协同工作承担外荷载。由于结构中存在拉线,精确的结构内力分析是非常复杂困难的。结构设计时常采用参考文献[1]中基于简化分析方法建立的计算公式,该方法是以门型构架为刚体,求拉线张力是以两主柱延长线交点为矩心列平衡方程,忽略了主柱横向荷载、柱脚横向支反力的作用,拉线变形和初应力、垂直荷载对横向位移的作用均不能考虑进去。这种作法与拉门塔的实际工作方式差异很大。
本文主要是根据拉门塔受横向荷载作用的变形特点,提出受力分析模型。建立设计计算公式时,把各种因素有效地考虑进去。导出的结构侧移与拉线截面的关系式及关系曲线有效地解释了拉门塔的主要工作特性,对拉门塔的工程设计及理论研究都具有重要意义。由于在推导中引入了拉线强度条件及拉线2刚好不退出工作的临界条件,使得拉线截面的设计选择更为简便易行,并用一个实际工程结构的简单计算验证了这一点。导得的计算公式可供设计参考和使用。
1 拉门塔的工作特点和简化假设
拉门塔结构在横向、垂直荷载作用下,产生一定侧移(Δ)后而保持稳定的平衡状态。这主要是由拉线和门型构架共同提供侧向抗力的结果。拉线是通过其张力的横向分量提供侧向抵抗力,门型构架是通过横担-主柱连接点抗弯提供侧向抗力。假如没有拉线,侧向抗力只能由门型构架全部提供,横担-主柱连接点需要传递较大的弯矩(与传递的剪力和轴力相比)。由于拉线的设置,给拉门塔的侧移提供了很大的抗力,而门型构架只分担很小一部分抗力,横担-主柱连接点只需传递较小的弯矩。此时,横担-主柱连接点主要表现为铰接特性(主要传递剪力、轴力、较小的弯矩)[2]。在实际设计的拉门塔结构中,横担-主柱连接点比较薄弱,抗弯能力较小,只能提供很小的弯矩抗力。
在实践中,对拉门塔实施精确内力分析是非常复杂的,分析技术难于掌握。因此,根据拉门塔的工作特点,在分析中,把横担-主柱连接点简化为铰接点,忽略了较小的弯矩抗力。这种作法给分析带来了很大的简化,同时各种因素可充分地考虑进去。
2 计算公式的建立
拉门塔结构如图1所示。取横担方向为x轴,垂直向上为z轴,与横担垂直的水平方向为y轴。设主柱长为H,其在x、y、z坐标轴上的投影分别为hx、hy、hz;设拉线长为L,在x、y、z轴上的投影分别为lx、ly、lz,拉线截面、弹性模量、初应力分别为AC、EC、σ0;横担-主柱连接点之间距离为a,拉线点距连接点距离为d;横担、主柱均为刚体。
图中,G为所有垂直荷载之和;P1为塔头部分所有横向荷载之和;P2为主柱风荷载。
如图2所示,在横向、垂直荷载作用下,拉门塔发生侧移Δ。此时,拉线1固定点F位移为( ),拉线2固定点E位移为(Δ, ),拉线2固定点E位移为(Δ, )。拉线1伸长为ΔL1 )。拉线1伸长为ΔL1
ΔL1=L′(变形后的长度)-L(初始长度)
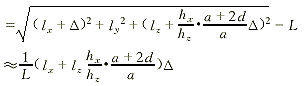
同理,可得拉线2的伸长量为
ΔL2=-ΔL1
拉线1、2变形后的张力为
 (1) (1)
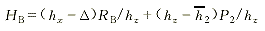 (2) (2)
对式(1),当Δ≥0时,始终有T1>0,说明拉线1始终参与工作。对式(2),当Δ<σ0/{(EC/L2)[lx+lz(hx/hz)(a+2d)/a]}时,有T2>0,此时,拉线2参与工作;当Δ>σ0/{(EC/L2)[lx+lz(hx/hz)(a+2d)/a]}时,T2<0,实际上拉线为柔性体,是不能承受压力的,此种情况说明拉线2已退出工作,即T2=0;而当Δ=σ0/{(EC/L2)[lx+lz(hx/hz)(a+2d)/a]}时,恰好有T2=0,说明拉线2刚好退出工作。下面就拉线1、2共同工作,拉线2退出工作(拉线1单独工作)两种情况进行讨论。
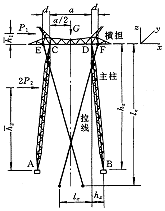
图1 拉门塔结构

图2 结构侧移稳定平衡状态
2.1 拉线1、2共同工作
横担脱离体各平衡方程(∑MD=0,∑MC=0,∑X=0)为
 (3) (3)
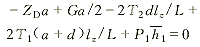 (4) (4)
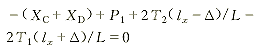 (5) (5)
两主柱平衡方程(∑MA=0,∑MB=0)为
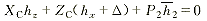 (6) (6)
 (7) (7)
式(6)+式(7)有
 (8) (8)
将式(1)~(5)代入式(8),整理后得侧移公式为
 (9) (9)
式(9)反应了侧移量与拉线截面的抛物线关系。由式(1)、(2),拉线强度条件和拉线2不退出工作,可建立2个不等式


整理后,有
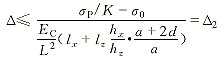 (10) (10)
 (11) (11)
式中,σP、K分别为拉线的破断应力和安全系数。
为满足拉线强度条件和拉线2不退出工作,式(9)的侧移量Δ必须同时满足式(10)、(11)。也就是要小于等于式(10)、(11)右端项中的最小值。
一般来说,钢绞线σP=1 176 N/mm2,K=2.2~3.0。这样由不等式(11)控制,即拉线2不退出工作要求的侧移较小。
将式(9)代入式(11),整理后得拉线1、2共同工作时所需的拉线截面为
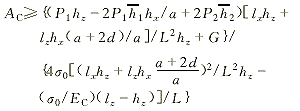 (12) (12)
式(12)中按等号计算出的截面为拉线2刚好退出工作时所需要拉线截面,用AC1表示。
2.2 拉线2退出工作,拉线1单独工作
如图2中拉线2退出工作时,T2=0。将式(3)、(4)、(5)中含有T2的各项去掉,然后将式(1)、(3)、(4)、(5)代入式(8),整理后得侧移公式
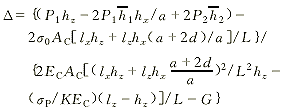 (13) (13)
式(13)反应了拉线2退出工作后,侧移与拉线截面的抛物线关系。
由于拉线2已退出工作,此时,不等式(11)失去控制意义,只有不等式(10)起控制作用。将式(13)代入式(10),有
 (14) (14)
按式(14)等号计算出的截面为刚好满足拉线强度条件所要求的拉线截面,用AC2表示。
柱脚支座反力(垂直RB,RA,横向HB,HA)及轴向力(NB,NA)由下式给出
 (15) (15)
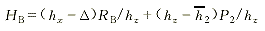 (16) (16)
NB=RB (17)
 (18) (18)
 (19) (19)
NA=RA (20)
若拉线2退出工作,式(15)、(18)中含有T2的各项应去掉。
3 拉门塔的工作持性曲线
根据式(9)、(13)的侧移Δ与拉线截面AC的关系,可得图3所示的拉门塔工作特性曲线。
图3中安全区段1为小侧移阶段,拉线变形较小,所以拉线2未退出工作。需要较大的拉线截面来保整个结构较大的侧移刚度。
安全区段2为大侧移阶段,拉线变形较大,拉线2已退出工作,拉线截面较小,结构侧移刚度较小。
不安全区段,拉线强度已不满足要求,结构可能发生失稳,设计时应予以避免。
图3中Δ1为拉线2刚好退出工作时的临界侧移;Δ2为拉线强度刚好满足要求时的临界侧移;AC1、AC2为临界侧移时所需的拉线截面。设计拉线时,可根据安全区段进行设计。

图3 拉门塔工作特性曲线
4 算例
220 kV拉门塔,结构几何尺寸:lx=4.5 m,lz=23.4 m,ly=11.5 m,L=26.46 m;hx=2.07 m,hz=20.7 m,hy=0;a=7.0 m,d=0。正常90°大风荷载:G=69 950 N,P1=26 600 N,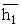 =0.6 m,P2=6 334 N, =0.6 m,P2=6 334 N, =10.35 m。拉线特性指标:EC=181 300 N/mm2,σp=1 176 N/mm2,σ0=160 N/mm2,K=2.2。 =10.35 m。拉线特性指标:EC=181 300 N/mm2,σp=1 176 N/mm2,σ0=160 N/mm2,K=2.2。
解
(1)按工作区段1设计拉线 [1] [2] 下一页
|


