基于FFT分析的故障诊断方法因系建立在信号的平稳性假设基础上，所以仅适用于平稳信号分析。而在工程应用中存在大量的非平稳信号，其频率成分及强度随时变化，如摩擦、松动、裂纹、油膜失稳等产生的故障信号，齿轮、轴承表面缺陷引起的调频、调幅信号等，必须采用能反映信号时变特征的时间一频率两维分析方法。此外，FFT分析其实质是一种线性变换方法，虽然大型旋转机组正常情况下大都可简化为线性系统处理，但是在故障状态下，有时也会表现出较强的非线性，此时FFT分析便不能正确反映信号中的全部信息。
    因此，出现了短时傅里叶变换、Wigner分布和小波变换等针对时变信号处理的分析方法，分形、混沌等处理非线性信号的分析方法，以及神经网络滤波、分形滤波、小波分解、奇异谱降噪等多种信号提纯方法，并在诊断实践中初见成效。本文介绍采用小波分析技术提取信号中蕴含的微弱冲击故障信号，大大提高了信噪比。现场应用情况表明，该方法可在强噪声环境下提取设备振动中的微弱故障信息，及时发现早期故障隐患。
    一、小波分析与神经网络滤波技术简述
    1．小波分析
    小波变换的基本思想与傅立叶变换是一致的，但其所用的正弦（或余弦）函数系不同，系由一基本小波函数的平移伸缩构成。
    小波函数系（WT）可以解释为（对每一分析频率fn）用具有中心频率f的带通滤波器对信号x(t)滤波的结果。
    小波Ψa，b所确定的窗口的形状和大小是变化的。│α│越小时宽越小，频宽越大。高频时，窗口自动变窄，低频时窗口自动变宽，因此非常适合于信号的时频分析。并且由于小波变换能够对信号的高频成分进行精细的刻划，因而被形象地称为对信号具有“显微”能力，被誉为“数学显微镜”，如图1所示。

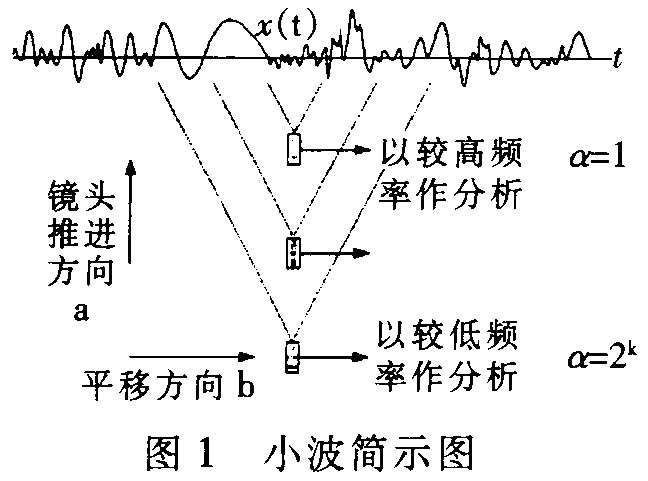
    由于小波分析可以在时一频域局部化，而且时窗和频窗的宽度可调节，故可检测到突变信号（在信号突变点处，小波变换的模取得局部极大值）；当进行多尺度小波分析时，随着尺度的增大，噪声引起的小波变换模减小，而故障引起的小波变换模得以明显显露，因此小波分析可以滤去信号中的噪声干扰。
    2．神经网络自适应滤波技术
    神经网络自适应滤波很少或几乎不要求对待滤波信号有任何的先验知识，而且滤波器的参数可以随信号的变化而改变，始终在最优的状况下进行工作。其原理如图2所示。

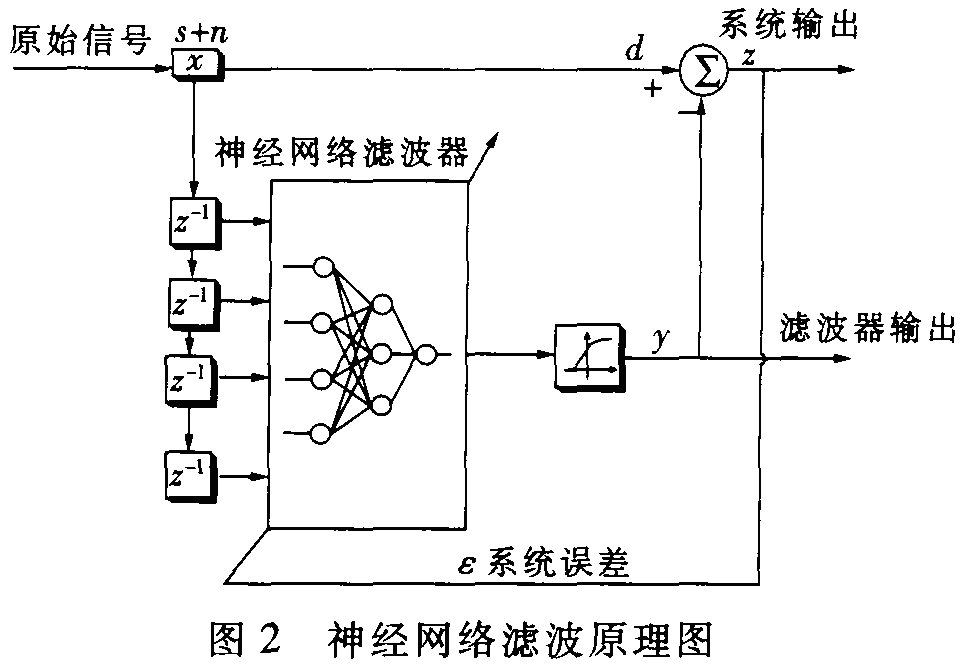
    由图可见，从传感器采集的信号：s+n经过系统分离后，分别作为滤波器的期望输入和参考输入。我们的目的是将参考输入信号经过神经网络滤波器后得到一个预测输出y，如果期望输出设为d，而网络的实际输出为y，对ε=d一y取数学期望，则ξ=E[ε2]扩。在训练过程中，网络权系的调整，就是使ξ达到最小。当训练满足要求后，滤波器的输出就是所要求的特征信号，而系统输入中的随机噪声就被滤掉。
    二、现场应用
    某催化炼化装置的烟机—主风机组，其增速齿轮箱的传动功率为4.6MW，低、高速轴的转速分别为1 486r/min和6 042r/min，齿数分别为114和28。
    该机组某次大检修后齿轮箱振动一直在4.0~7.0mm/s之间波动，振值虽然较大，但无明显上升趋势。图3是低速轴的原始振动波形和频谱（当时壳体振动烈度值为6.0mm/s左右），除了啮合频率(2.8kHz)处有一较大峰值外，很难从中得到更多有益的启示。

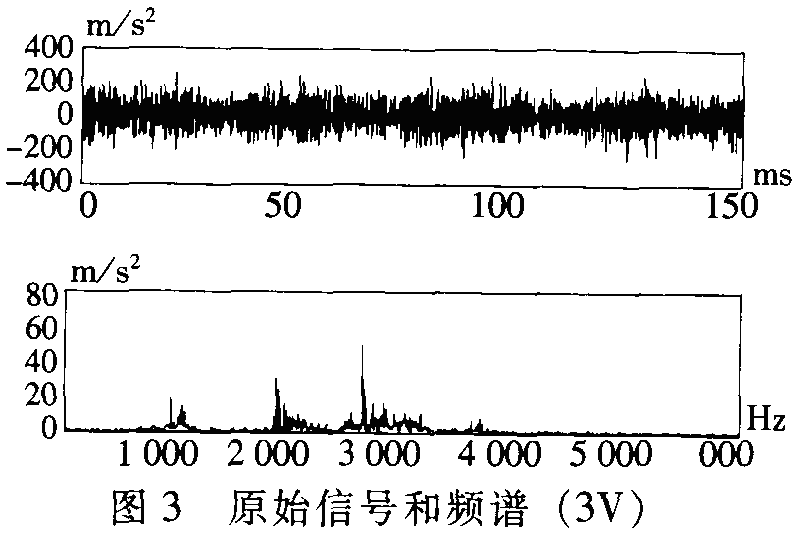
    图4是经小波分解后的波形和频谱，从中可看出在160ms的时间跨度内存在四个明显的脉冲，但时间间隔不一样。

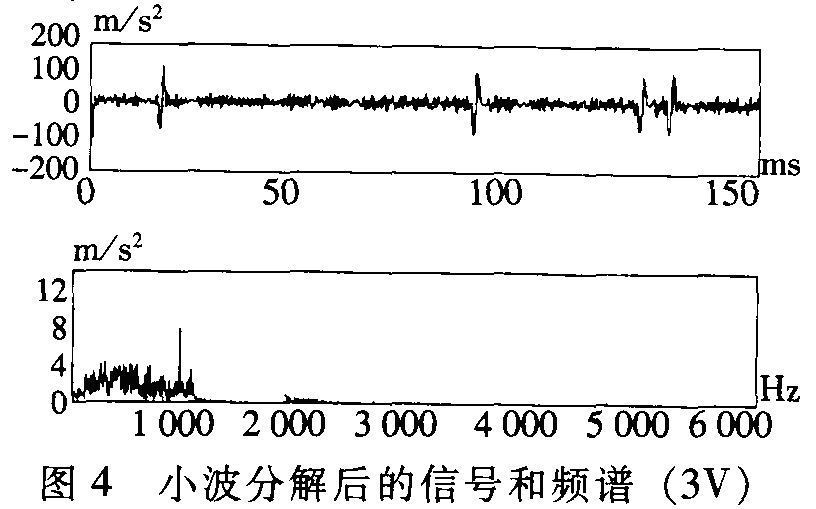
    图5是经神经网络滤波后的波形，其结果与小波分解后的结果完全相同，也存在四个随机冲击。
 

    图6是高速轴的振动经小波分解后的波形和频谱，也存在很明显的随机冲击形象，且脉冲的数量更多。

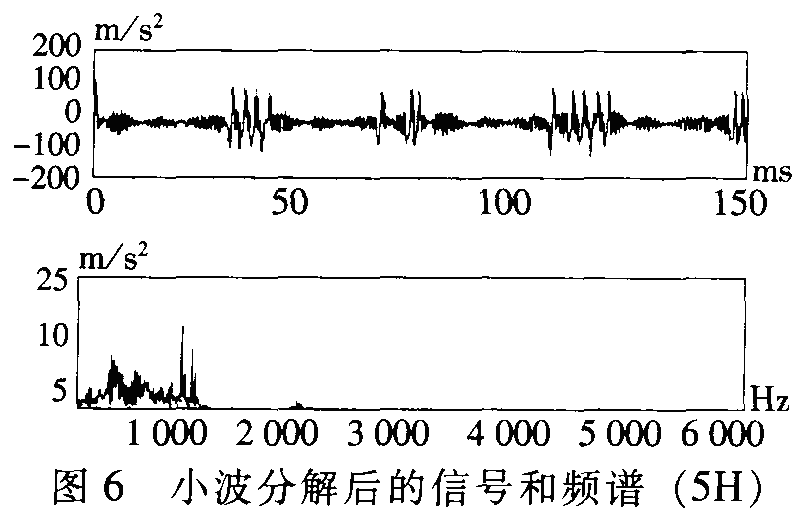
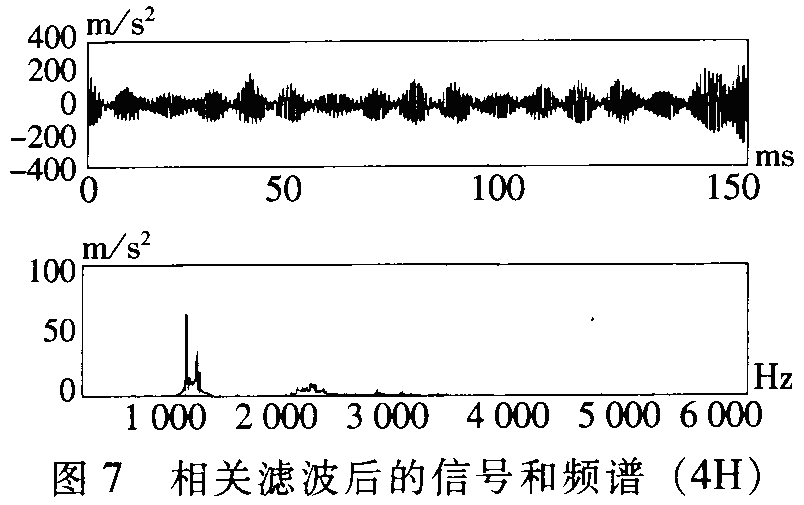
    图7是齿轮箱低速轴振动经相关滤波后的振动波形和频谱，由图可见，存在明显的调幅现象。

    综合分析认为，该齿轮箱存在明显的随机冲击现象，很可能是由于轴瓦巴氏合金剥落，或润滑油中有较多的杂质造成。同时从齿轮箱轴向振动较大及调幅特征明显的现象看，可能还存在安装不平行及齿面磨损的缺陷。
    此后，又对齿轮箱的润滑油样进行了铁谱分析，证实存在较大尺寸的巴氏合金颗粒。
    在齿轮箱最高振值上升至9.5mm/s时停机揭盖检查，发现四副轴瓦中有三副已发生较严重的瓦面巴氏合金剥落和裂纹，同时齿面存在磨损痕迹。
    由此可见，应用小波分析、神经网络滤波等方法对齿轮振动进行降噪处理，可大大提高信噪比。在停机前约两个月，壳体振值尚无明显异常的情况下，有效地提取出了当时还很微弱的故障信息，为生产决策和运行维护提供了科学、宝贵的依据。

    参考文献：
    [1]徐金梧，张晓彤等．神经网络滤波器在故障中的应用[J]．
    [2]徐金梧，徐科．小波变换在滚动轴承故障诊断上的应用[J]．机械工程学报，1997，33．