王洪泽
广西电力有限公司,南宁530023
0 引言
220 kV西南线#23塔(图1)A相导线遭受雷电绕击,强大的雷电流造成A相闪络后沿铁塔入地,C相反击,使C相瓷瓶串闪络[1]。
核算表明,该#23塔的地面倾角θ=-23.3°,耐雷水平I1=775~94.9 kA。据此估算,注意到C相反击闪络,绕击A相的雷电流将高达94.9 kA,相应最大击距为216 m。
由于Whitehead和Brown的最大击距公式不适用于θ<0和K<1的情况,因此,用文[2]提出的最大击距通用公式来分析94.9 kA大雷电流绕击#23塔A相导线的可能性,并从物理概念分析电气几何模型的最大击距。
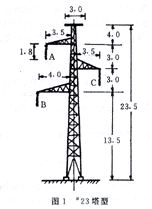
1 94.9 kA雷电流绕击导线的条件
1.1必要条件
#23塔的结构参数、导线和避雷线的布置状况以及地表环境等因素能够确保该塔具有最大击距rsm,且rsm>rsc(rsc为临界击距),此即必要条件。
假如所研究的线路没有一个最大击距,则从物理意义上看,就是该线路的避雷线对导线(或某相导线)不起保护作用。显然,这种情况下的线路与无避雷线的线路等效,实际上无“绕击”,而是直击。这表明任何雷电流或大雷电流都有直击导线的可能性。
1.2充分条件
设线路某铁塔段已满足必要条件,则塔段所固有的最大击距须≥给定的最大绕击雷电流Ism所对应的最大击距rs=f(Is),即rsm≥rs=f(Is)|Is→Ism。因雷电流Is与击距rs的关系为[3]:
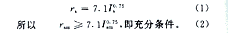
式中,rsm为铁塔段考虑环境影响时所固有的最大击距,m;Ism为最大绕击雷电流,kA。
例如,对于Ism=94.9≈95 kA大雷电流绕击#23塔A相导线的命题,就须按式(2)证明该塔段存在最大击距为:rsm≥7.1×950.75=216(m),命题才得证。
2 最大击距通用计算公式
我们提出的最大击距通用计算公式为[2]:

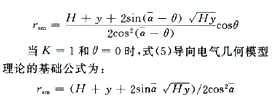
值得注意的是:1)α和θ有符号,α以基准轴反时针方向通过导线为“+”,反之为“-”;θ以杆塔处水平地面为基准,向下倾斜θ为“-”,反之为“+”。2)K的物理意义是雷击导(地)线的平均临界电场强度对雷击地面的平均临界电场强度之比。
3 95 kA大雷电流绕击A相导线的验证计算
A相14×C—5绝缘子串的50%冲击放电电压U=1 300 kV,导线阻抗Z=375Ω,线路的绕击耐雷水平Isc=2U/Z=6.93 kA。与其对应的临界击距由式(1)可得:Isc=7.1×6.930.75=30.3(m)

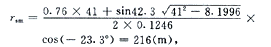
与其对应的最大绕击雷电流由式(1)求逆可得Ism=95 kA>Isc=6.93 kA。由此可知,95 kA大雷电流绕击A相导线并造成闪络是可能的。
4 通用公式无解的物理意义
式(3)无解的条件是:F≤0。
以#23塔为例,假如K值采用文[5]推荐值取K=0.53,则由式(3)得:
F=0.532-sin242.3°=-0.172<0
即式(3)无解,其物理意义是#23塔A相导线无最大击距。
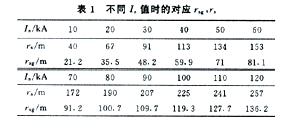
如用电气几何模型作图,则雷电对地击距rsg=Krs,rs按给定的雷电流由式(1)计算。取K=0.53时 ,各种雷电流情况下,rs和rsg值见表1。由此作出电气几何模型见图2。可见暴露弧线随雷电流Is的增大而增大,始终存在着暴露弧段即没有最大击距rsm。如此电气几何模型的图解分析结果与式(3)解析一致 。

5 式(3)无解的正确处理
假设取K=0.53合理,则式(5)无解。这时,较好的办法是减小保护角α(如确认K=0.53偏小,应增大K值,再试选α值)。取α=2.9°,K=0.53时,类似于第3节计算得rsm=214 m,相应的最大绕击电流Ism=94 kA。与计算结果比较,两者的绕击特性大致相当。但本节取K=0.53的造价增大。由此可知,选择合理的K值是值得研究的问题。
6 结论
a.用本文给出的充分、必要条件来分析大雷电流绕击导线命题时,可避免误证。
b.95 kA大雷电流绕击#23塔A相导线的可能性存在。
c.式(3)无解即无最大击距时,表明避雷线对该相导线无保护作用,应当重新设计。
参考文献
1 李如虎.西南线#23塔雷害事故的分析.高电压技术,1985,(3):67
2 王洪泽.导线和地面临界电场强度不相同时雷电最大击距的计算公式.中国科学技术文库(电工技术 ),北京:科学技术出版社,1998
3 冯宝忆.输电线路避雷线屏蔽效果的计算.高电压技术,1980,(2):46
4 章润陆,陆宠惠,李劲波.输电线路绕击率的探讨.高电压技术,1985,(1):39
5 李如虎.对E.R.whitehead电气几何模型的进一步推导.雷电与静电,1989,(2):8
|


