谷 毅,赵玉柱,张国威,刘 皓,陈 刚
国家电力调度通信中心,北京100031国家电力调度通信中心,北京100031
1 引言
根据500 kV阳城电厂送出工程系统调试方案(江苏部分第二、三阶段)的安排,2000年2月20-22日,500 kV阳城电厂送出工程启动验收委员会在东明开关站主持了500 kV东明开关站启动调试工作。本次调试共有五个调试项目[1],在进行第一项“东明站带4组高抗零启升压”试验之前的系统方式调整时,投入任庄变电站2号联变的1号低抗后,处于备用状态的三堡—任庄线路(堡任5231线)两侧CVT显示有电压560~570 kV,现场将1号低抗退出运行后,电压消失,估计是产生了电压谐振。本文通过实际计算和理论分析,证明这一现象确是由于参数设置不当而发生了串联电压谐振,在较低的互感电压作用下,产生很高谐振电压的结果。
2 系统状态
谐振发生前的系统状态如图1所示,任庄变2号联变220kV侧开关2012、2013冷备用,三堡站5031、5032开关冷备用,2号联变分接头位置:500/208.59/36kV。堡任5231线与当时正在运行的任庄—上河线路(任上5237线)有一段7km左右的同杆并架线路,在操作投入2号联变一组低抗时,系统发生谐振。从现场取得的系统结构参数如下:
线路总长为36.89km,与5237线同杆并架长度为6.79km,同杆并架起点距任庄侧长度为11.624km,线路电阻、电抗、对地电容和互感电抗分别为0.762Ω、10.051Ω、0.5µF和8.668Ω。
任庄2号联变铭牌参数:高压绕组/中压绕组/低压绕组额定容量为167/167/66.7MVA;以167MVA为功率基值时,高、中/高、低/中、低侧的短路电压分别为11.54%、35.95%、19.5%;额定电压为525/230/36kV时,高、中/高、低/中、低侧的铜损分别为237 kW、177.2 kW、174kW。
1号低压电抗器额定容量为45Mvar,额定电压为36kV。

3 建模与计算
根据系统状态,建立如图2所示的系统模型。由于500kV主干网中,电阻远小于电抗,因此,建模时电阻忽略不计。图中各件定义如下:
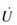
X高、X中、X低:为2号联变500 kV、220 kV、36 kV侧绕组的漏抗;(以下除特殊说明外,各结构参数和运行参数均为标幺值,系统功率基值取167 MVA,电压基值取相应电压等级的平均额定电压[1]);XLL:为低压电抗器的电抗值,j3.711;K*为2号联变500kV侧非标准变比,1.05;XBRr、BBRr为堡任5231线任庄侧线路电抗、对地电纳,XBRr=j0 .001918,BBRr=j0.0816;XBRt、BBRt为堡任5231线与任上5237线同杆并架段的线路电抗、对地电纳,XBRt=j0.00112,BBRt=j0.0477;BBRb为堡任5231线三堡侧线路对地电纳,BBRb=j0.1298; 、XM为任上5237线对堡任5231线的感应电压、互感电抗, 、XM为任上5237线对堡任5231线的感应电压、互感电抗,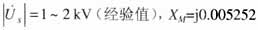 ; ; 为堡任5231线任庄侧电压。 为堡任5231线任庄侧电压。
经Y/Δ变换,消去节点B,并进行并联支路导纳合并,串联支路阻抗合并等处理,可得系统等值电路如图3所示。
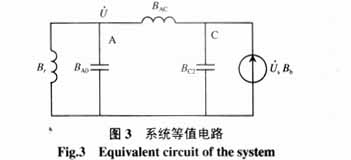
图3 系统等值电路
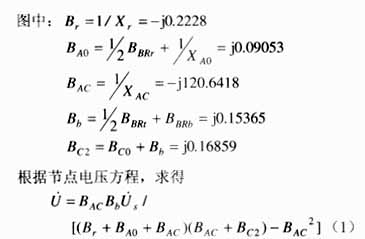
定义谐振电压比 ,则在上述现场取得的系统结构参数下,运行于工频f=50.0Hz时,U* =4.2108。通常情况下,对于非全线同杆并架的线路,位于线路两端的测量点(PT安装点)远离同杆并架点,测量点与同杆并架点之间的线路阻抗所引起的压降,使测量点电压幅值低于同杆并架点的感应电压幅值,即U*<1;对于全线同杆并架的线路,U*=1。而发生电压谐振时,因系统感性参数与容性参数相配合,使得幅值较小的感应电压 ,则在上述现场取得的系统结构参数下,运行于工频f=50.0Hz时,U* =4.2108。通常情况下,对于非全线同杆并架的线路,位于线路两端的测量点(PT安装点)远离同杆并架点,测量点与同杆并架点之间的线路阻抗所引起的压降,使测量点电压幅值低于同杆并架点的感应电压幅值,即U*<1;对于全线同杆并架的线路,U*=1。而发生电压谐振时,因系统感性参数与容性参数相配合,使得幅值较小的感应电压 在谐振电路中产生很大的谐振电流,从而在各元件上产生幅值很大的谐振电压 在谐振电路中产生很大的谐振电流,从而在各元件上产生幅值很大的谐振电压 。因此,从理论和实践中,都可用谐振电压比U*>1作为判断同杆并架线路发生电压谐振的依据。根据上述计算可以判定,试验系统在该运行方式下,确实是发生了串联电压谐振。 。因此,从理论和实践中,都可用谐振电压比U*>1作为判断同杆并架线路发生电压谐振的依据。根据上述计算可以判定,试验系统在该运行方式下,确实是发生了串联电压谐振。
该系统在将联变所带低抗退出运行后,谐振电压比U*=0.06732<<1,不会产生谐振,与现场实际观察情况完全吻合[1],这也再次证明了用“谐振电压比U*>1”作为发生电压谐振依据的正确性。
4 谐振产生分析
由图3所示的系统等值电路知,如果该电路任庄侧电纳Br与任庄侧线路等值自电纳BA0并联结果(Br+BA0= - j0.1323)与任庄(A点)、三堡(C点)间等值互电纳BAC、三堡侧线路等值自电纳BC2参数配合,则发生串联电压谐振。此时有
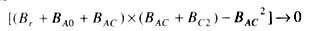
即谐振电压比U*→∞,所以,根据试验时观察堡任5231线线路两端电压560-570kV,而一般情况下,长度为6.79km的同杆并架线路,感应电压通常为1-2kV的经验值可推知,当时该线路正是发生了串联电压谐振,这也与“串联谐振将产生设备过电压[3]”的论述是一致的。
由于低抗、联变等设备铭牌参数的准确性较高,而线路参数往往由电建部门实测,其测量时系统状态、沿线空气湿度等客观因素对测量结果影响,特别是对线路电容影响较大。因此,若认为所给线路的对地电容参数有一定的误差,则可进一步用理论推导验证在当时状态下,串联谐振会发生。这种参数调节,若其幅度较小,例如在15%以内,可以认为是与实际情况相符合的。而这种参数调节是为了更好地验证串联谐振的发生,因为即使按照目前所给实测值,上述计算也已很好地说明了在当时状态下,系统发生串联谐振的情况及发生条件。
假设线路电容实际值比实测值减小13.9%,即堡任5231线对地总电容由0.5μF减小为0.4305μF,即
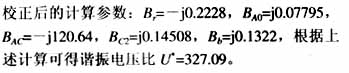
以500kV线路有6.79km同杆并架,感应电压在1~2kV这一实际运行经验值为例,在该系统参数下,堡任5231线任庄侧电压计算值与实际观察值十分接近,这也更好地说明在当时状态下,系统出现过电压是由于串联谐振引起的。
5 串联谐振点的分析

式中 Leq、LAC、C2分别为Beq、BAC、Bc2对应的等值电感和等值电容。
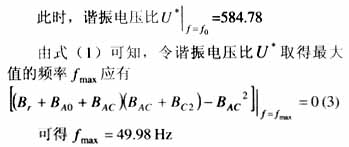
由上述计算可知,当谐振频率f0≈fmax时谐振电压比具有最大值。这是由于为简化计算,未考虑系统的电阻,若考虑系统电阻R,则f0<fmax,R越小,两者越接近。
6 谐振电压在谐振点附近的频率变化特性
电力系统发生串联谐振时易产生过电压,造成设备损坏,因此对电力系统规划设计和运行人员来说,都有必要采取措施避免谐振产生。上述3~4已经讨论了系统结构参数对产生谐振的影响,合理设置系统结构参数是避免谐振产生的根本途径,在电力系统规划设计阶段和制定运行方式时,应当充分考虑到这一问题。但在某些特殊情况下,可能由于种种需要而难以避免参数设置符合谐振条件,例如本文所提到的东明站调试阶段,安排系统方式时,参数偶然符合谐振条件,此时为避免谐振的发生,如条件允许可以适当调节系统运行频率。因此,有必要讨论谐振电压在谐振点附近的频率变化特性。
考虑谐振电压比U*对系统圆频率ω的全微分,由式(1)可得

根据式(4),谐振电压比U*在不同系统运行频率下的变化率为:
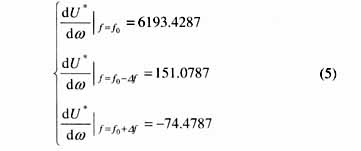
变化率之比

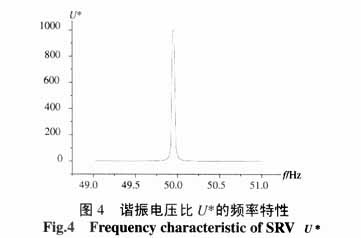
根据上述极值分析和函数连续性分析,可知谐振电压比U*对系统运行频率的函数图象大致如图4所示。
[1] [2] 下一页
|


