0　引言

　　电力系统的实时运行和控制需要了解系统的真实运行工况，由于测量和传输等方面的原因，得到的生数据难免存在误差，甚至是坏数据。状态估计能在一定程度上提高数据的精度。状态估计软件是能量管理系统的一个重要组成部分，紧急控制系统中也需要状态估计软件^［1］。
　　加权最小二乘法(WLS)是电力系统状态估计中应用最多的算法，其中面向行处理、基于二乘Givens变换的正交变换法被认为是最好的算法之一。对于严格服从正态分布的量测数据，WLS估计结果具有方差最小且无偏的统计特性，WLS的数学模型简洁，计算方法简单，但却不具备抗御坏数据(估计理论上称之为粗差)的能力。状态估计中坏数据的检测与辨识问题至今尚未得到完全解决。为了提高状态估计抑制坏数据的能力，提出了非二次估计准则(non-quadratic criterion)^［2，3］，其中加权最小绝对值(WLAV)估计准则是广大学者研究最多的非二次估计准则之一，近来受到许多学者的关注^［3～5］。WLAV属于L₁范数估计，L₁范数估计具有很强的抗御坏数据的能力^［6］，在电力系统状态估计中，在检测辨识坏数据和抑制坏数据方面，WLAV与WLS相比具有较好的性能^［3，7］。求解WLAV问题的方法大多是基于线性规划和非线性规划的内点法(interior point method,缩写为IPM)^［3］，计算工作量大，较难检测、辨识并抑制杠杆量测中的坏数据，不利于它的实时应用。
　　WLS和WLAV各有优缺点，它们估计性能的优劣与生数据的误差分布特性有关，研究估计算法，将两者的优点综合于一体是有益的探索，追求的目标是对WLS软件进行少量的修改，略增加计算量，使之具有一定的抑制坏数据的能力。

1　基本算法

　　电力系统状态估计的量测方程是：

z=h(x)+v

(1)

其中　z是m×1量测矢量；x是n×1状态矢量；h(^.)是m×1非线性量测函数；当x是真值时，v是m×1量测误差矢量；当x是估计值时，v是m×1量测残差矢量。
　　状态估计就是由量测值按估计准则计算状态变量，使目标函数最小。WLS估计的目标函数为：

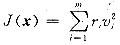
(2)

其中　r_i是量测i的权；v_i是量测i的残差。
　　WLAV估计的目标函数为：

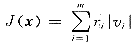
(3)

式(3)可变为：

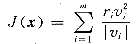
(4)

令

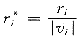
(5)

则式(4)可写成与式(2)类似的形式：

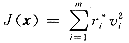
(6)

　　式(5)中的r*_i是量测i的残差的函数，称为权函数(weight function)^［6，8］。这样，借助权函数的概念，建立了WLAV问题与WLS问题之间的联系，用求解WLS的方法求解WLAV问题，在此基础上综合两种方法的优点，这是基于权函数的电力系统状态估计算法的基本着眼点。从理论上讲，该算法与用其它方法(如线性规划和非线性规划)求解WLAV问题得到的估计结果相同，实际上会存在一些差异，这是由不同的计算方法引起的^［8］。
　　基于权函数的电力系统状态估计算法(function weighted least squares,缩写为FWLS)与通常的WLS方法的唯一区别是：该方法在求解迭代过程中量测的权值随量测残差而变化，而WLS在迭代过程中量测的权值是固定的，由先验的统计信息确定。因此，仅需对常用的WLS估计软件作很少的修改，就可实现该算法。
　　用FWLS求解状态估计问题时，开始先用给定的量测权值，固定不变，用求解WLS问题的算法迭代若干次；然后根据残差用权函数计算量测的初始权值；接着进行量测权值随残差变化的迭代，每次迭代前修改量测的权值，直到满足收敛要求，此时仍是用求解WLS问题的算法进行迭代。当量测数据中存在坏数据时，一般，坏数据对应的量测残差的绝对值比其它量测残差的绝对值要大，在迭代过程中，与正常量测对应的量测权值相比，坏数据对应的量测权值不断减小，这样在一定程度上抑制了坏数据对估计结果的不良影响。在量测数据正常时，FWLS与WLS的估计效果基本相同，在量测数据中有坏数据且不能得到有效排除时，FWLS的估计准确性比WLS高，试验也证实了这一点。

2　改进算法

　　在用FWLS求解时，可能出现迭代若干次后残差绝对值下降速率很小，而残差绝对值依然较大，因而收敛慢，尤其是量测数据中有坏数据时较为明显。由式(5)，r^*_i的微分为：

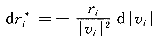
(7)

　　随着迭代次数的增加，|-d|v_i||愈来愈小，|dr^*_i|也愈来愈小，迭代计算近乎停滞不前，目标函数收敛变慢，迭代计算的次数增加^［9］。为加快收敛速度，减少迭代次数，考虑在适当时侯，改变量测权值的变化量。在迭代过程中，量测残差是很重要的信息，量测残差的变化量也是十分重要的信息，将它作为因子调整量测权值的变化量，对于那些量测残差绝对值较大，且两次迭代残差绝对值变化很小的量测，对其权值进行如下修正：

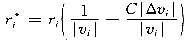
(8)

其中　Δv_i是第k次迭代与第k-1次迭代量测i的残差之差；C是大于0的常数。
　　在估计迭代过程中，迭代若干次后，那些量测残差绝对值较大且两次迭代残差绝对值变化很小的量测是坏数据的可能性一般较大，因此，进一步减小其权值。
　　在实际估计过程中，前几次迭代用的权函数直接用式(5)中的r^*_i，并不需要修正，在后继迭代过程中，也不是所有的量测权值都进行修正。改进算法在基本算法上增加的计算工作量不多，但加快迭代收敛速度的效果十分明显，求解迭代计算的时间明显减少，其效果与选择的常数C有关。另外，在迭代过程中，量测残差的变化信息不仅可用来加快收敛速度，也可作为检测与辨识坏数据的重要信息。

3　算例

　　为检查本文提出的电力系统状态估计算法的估计效果，用IEEE 30和IEEE 118节点系统数据进行试验，比较基本算法、改进算法和WLS三种方法估计结果的准确性。在多种量测条件下进行试验(如改变量测冗余度，量测数据只有噪声，量测数据中除噪声外还有坏数据等)，将3种方法的估计结果与真值分别进行比较。用以下的指标来衡量估计的状态变量的准确性^［7］：

(9)

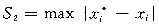
(10)

其中　x^*_i是估计的第i个状态变量；x_i是第i个状态变量的真值；i=1,2,…,n。
　　试验中的状态变量真值和量测真值是根据IEEE 30和IEEE 118节点系统数据用BPA潮流程序计算得到的，在量测真值上随机加入2%的高斯噪声得到不含坏数据的生数据，通过将生数据改变符号，将生数据置零，生数据位置调换和按比例系数同时改变某一量测点的有功和无功数据，得到试验用的坏数据，基本上与实际系统中产生的坏数据的特征相吻合。试验时，坏数据中有支路量测也有节点注入量测，有单个坏数据、多个不相关坏数据和多个相关坏数据。求解WLS的方法采用文献［10,11］介绍的利用稀疏技术基于二乘Givens变换的正交变换法。在求解WLS过程中，采用定雅可比矩阵，只进行一次Givens变换。基于权函数的算法在求解过程中也是采用定雅可比矩阵，但每一次修改量测权值后，重新进行Givens变换。本文在DECpc LPx⁺ 466d2微机上进行试验，表1和表2列出了IEEE 30节点系统的试验结果。
　　从表1和表2可看出：对IEEE 30节点系统，没有坏数据时，基本算法和改进算法与WLS的估计准确性基本相同。有坏数据时，基本算法和改进算法

表1　IEEE 30节点系统状态变量估计的准确性比较
Table 1　Comparison of estimation accuracy
of state variables among three methods
(IEEE 30 system)

表2　IEEE 30节点系统3种方法的迭代次数
和计算时间比较
Table 2　Comparison of iteration count and calculation
time by use of different methods (IEEE 30 system)