汤振飞 单渊达
东南大学电气工程系 210096 南京
0 引言
一个电力系统具备可观察性,系指系统的测量数量、种类、分布足够用以求解系统当前的状态。总体上讲可观察性分析有如下几方面的问题需要解决:首先要进行可观察性判断,如果系统已判断为可观察,则可以进一步进行测量后备重数及安全度的分析,并进而分析如何择优增加测量使得系统的安全度进一步提高;如果系统已判断为不可观察,则需要将系统划分为若干个可观察岛,并可进一步分析如何择优增加测量,以提高系统的可观察性。
本文在分析测量之间线性相关的基础上提出了线性相关环的概念,并利用线性相关环来系统地解决可观察性分析的这些问题。
1 线性相关环概念的提出
1.1 测量向量、测量矩阵及DC状态估计器的概念
对于一个n节点、m测量的系统,每个测量形成一个测量向量h,h中各元素之和为0,以h为行向量组成测量矩阵H,将H线性化即得DC状态估计器。
采用P—θ有功模型,测量向量h表达式为:
h=[f1,f2,…,fk,…,fn]
若h为节点i的注入测量向量,则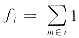 , m为与节点i有连线的节点;k为与节点i有连线的节点时,fk=-1;k为其他节点时,fk=0。 , m为与节点i有连线的节点;k为与节点i有连线的节点时,fk=-1;k为其他节点时,fk=0。
若h为节点i与节点j之间的支路测量向量,则fi=1;fj=-1。
对于P—θ有功模型的分析方法同样可以应用于Q—V无功模型的分析。
本文的分析都是以这些概念为基础的。
1.2 线性相关环的概念
定义1 对任意一组测量向量h1,h2,…hl,若满足k1h1+k2h2+…+klhl=0(k1,k2,…,kl均不等于0),并且若去掉这组测量向量中的任何一个向量(不妨设为hi),都不能满足c1h1+…+ci-1hi-1+ci+1hi+1+…+clhl=0(c1,…,ci-1,ci+1,…,cl为任意不等于0的实数),就称这组测量向量构成一个线性相关环(以下简称为环)。其中k1,k2,…,kl称为关联系数。图1为几个典型环的拓扑图。
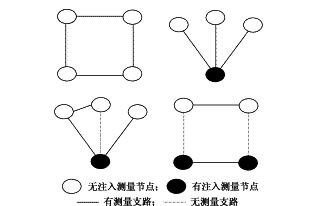
图1 几个典型环的拓扑图
Fig.1 Topologic graphs of some typical loops
环具有以下特点。
a.环的消元特点:以一组构成环的测量向量h1,h2,…,hl为行向量构成测量矩阵H=[h1,h2,…,hl]T,对H矩阵进行高斯按列消元,则第l行必全为0。
b.一个环中各个测量相互后备,其中任一个测量的失去都可以由环中其它的测量线性组合得出。可见一个环就代表一个冗余成分,环有效地表示了系统的后备情况。
c.环的基本操作有两种:解环和合环。
解环操作:对任何一个环,去掉环中任何一个测量就完成了解环操作。该环余下的测量相互线性独立,但也有可能与其他测量构成新的环。
合环操作:对构成最小支撑树的一组测量,任意增加一个测量都必然与这组测量的部分或全部合成一个环。
1.3 广义最小支撑树的概念
定义2 一个不构成环的最大的测量集中的测量称为基测量,基测量之外的测量称为对于这个基测量集的冗余测量。n-1个基测量组成一个广义的最小支撑树(minimum spanning tree,简称为MST)。
对一组基测量,任意一个冗余测量都必然与这组基测量的部分或全部组成环。
定理1 系统可观察存在一个广义MST基测量的数目等于n-1。
广义MST形式上不一定张满所有节点,如果用拓扑法进行分析操作,广义MST必然是恰好能够张满所有节点的满秩的树。因而拓扑法传统的支撑树概念与广义MST是内在统一的。从第2.1节可见,可观察性判断数值法实质上也是在验证是否存在一个广义MST,因而可观察性判断的数值法与拓扑法在广义MST上得以统一。
定理2 (逢环必解定理)对于一个测量系统,对其中存在的每一个环进行解环操作,直到无环可解为止,则此时余下的测量全部是基测量。若其个数为n-1,则这些测量就构成了一个广义MST,由此可以判断该系统是可观察的。
对于一个可观察系统,广义MST往往不是唯一的。对于一个测量设置较为丰富的系统,广义MST的数量是很多的。基测量与冗余测量的划分也完全是相对的。
定理3 (广义MST演变定理)对于一个已可观察的测量系统的某个广义MST,取任一个该广义MST之外的一个测量(冗余测量,设为hr)加入到该广义MST中,则hr将与构成该广义MST的基测量的部分或全部合成一个环,去掉该环中的任意一个基测量成分(设为hb(k)),则又重新组成了一个新的广义MST。此时hr成为基测量成分,而hb(k)成为冗余测量成分。
由广义MST演变定理可以从一个广义MST逐步演变出全部可能的广义MST集合。其操作可以运用数值方法通过修正关联系数来完成[1]。
2 环在可观察性判断中的应用
2.1 对传统数值法的改进
传统数值法是通过对信息矩阵G=HTH进行三角分解,检查分解过程中是否出现0主元来判断可观察性[2]。根据逢环必解定理,可以通过对H矩阵直接分解来判断可观察性。
由于H=[h1,h2,…,hm]T,对H进行列选主元高斯按列消元,利用第1.2节介绍的环的消元特点,当消元进行到某个环的最后一个成员向量时,该行必全为0,这时通过列选主元将该行换至后边,亦即完成解环操作。整个高斯消元过程就是逢环必解的过程。消元结束后,H矩阵前边不全为0的行就都是基测量向量,后边的全0行就都是冗余测量向量。如果这些基测量向量数目达到n-1个,就构成了一个广义MST,此系统是可观察的,否则就是不可观察的。判断为可观察后还可以进一步得出各个冗余测量向量与基测量向量的关联系数。
2.2 对传统拓扑法的改进
传统拓扑法是通过检查支撑树能否张满所有节点来判断可观察性的[3],比较适合于人工方法进行分析。为了便于用计算机进行分析,本文采用大节点合并方法进行可观察性判断。
将所有存在支路测量连接的节点合并成为一个节点(称为大节点super bus,相应地原有节点称为小节点)[4],这其实就是一个局部可观察范围。参见图2。
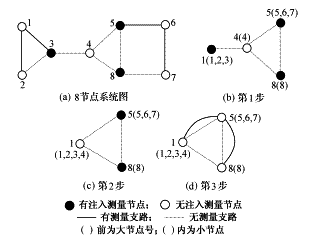
图2 大节点合并拓扑法操作示意图
Fig.2 Schematic diagram of super bus combination
第1步:以某小节点为中心出发,搜索所有存在支路测量相连的节点,并合并成为一大节点。然后从此大节点之外一节点仍作上述搜索、合并操作,直到整个系统不存在支路测量为止(如图2,支路测量1—2,1—3将节点1,2,3合并成为大节点1;支路测量5—6,6—7将节点5,6,7合并成为大节点5)。检查此时系统存在的大节点个数,若只有一个大节点,则已经可观察,否则进入第2步继续分析。
第2步:扫描各个小节点的注入测量,检查该小节点注入测量关联的支路个数(此时不存在支路测量),若等于1,则该节点注入测量可以等效地转换为该支路测量(图2中小节点3的注入测量转换成为支路测量1—4),又可进行节点合并操作;若多于1,则不可唯一转换,留待第3步处理。
第3步:扫描第2步余下的各小节点注入测量。检查该小节点注入关联的支路个数,若大于1,则任取其一支路作为该节点注入转化对象,成为伪支路测量,继续作大节点合并操作(如图2,节点5,8注入测量分别转换成为伪支路测量1—5,5—8)。若等于0,则情况较复杂,要回到该大节点内部去寻找所有与该小节点相关的环,检查该环路上有无已作伪支路测量处理的节点注入测量,如有则看能否将其调整至通向本大节点之外的支路,若可以则作此调整,并继续合并,否则检查其他环路;如所有环路检查后都不能调整,则该节点注入测量只能是冗余测量。
应用上述方法,若最终能合并为一个大节点,则系统是可观察的,否则不可观察。从算例执行情况看,对测量较富裕系统,如对连云港电网测量系统,第1步操作已判断为可观察,效率很高。对图2的8节点系统,第1步完成后只剩下4个节点,这样大大地缩小了系统的分析规模,便于下一步分析。对IEEE 14节点模型则到第3步才得出结论。
2.3 拓扑法与数值法相结合
大节点合并拓扑法基本操作是搜索与合并,整个过程不涉及浮点数运算,计算量很小。能够满足实时性要求。同时大节点合并拓扑法处理流程较为灵活,不一定要所有步骤进行完才有结论,因此也提高了效率。其不足之处是:第3步对于节点注入测量的分析逻辑较为复杂,对复杂网络处理不方便。
数值法的优势是:比较适合于计算机分析,编程较简单。其不足之处主要是:整个过程全是浮点数运算,且运算次数较多,对网络计算机机时开销较大。
针对拓扑法与数值法在可观察判断中的优缺点,本文提出将两者有机结合,优势互补,以满足可观察性判断在线应用的实时性要求。具体步骤如下。
第1步、第2步仍采取第2.2节大节点合并拓扑法的前2步,若还没有得出结论,第3步换用数值法进行分析:以第2步得到的大节点为单位形成H矩阵,然后应用第2.1节的列选主元高斯消元法判断可观察性。这样处理既克服了拓扑法对节点注入测量处理不力的缺陷,又极大地减少了数值法的计算量。算例表明,该办法可以快速、简单地解决问题,适合于在线应用。
3 测量后备重数的分析
定义3 某个测量的后备重数反映了该测量的关键程度,即失去该测量后对整个系统可观察性的影响程度。它取决于网络的拓扑结构和测量的分布。
孤立测量:即后备重数为0的测量,又名关键测量。失去该测量将导致整个系统不可观察,是对系统可观察性影响最大的一类测量。
一重后备:失去该测量不会破坏系统的可观察性,但会因此而在系统中出现新的孤立测量。
二重后备:系统不会因为失去该测量而出现新的孤立测量。
孤立测量说明该测量不与其它任何测量构成环,孤立测量必然是基测量。一重后备说明该测量与其它测量构成一个环。多重后备说明该测量关联的环不止一个,失去该测量后其他测量仍旧合并成环,不会形成新的孤立测量。运用线性相关环的概念可以很好地进行测量后备重数的分析,并进而求取m-k级安全度(k=1,2)。
4 择优增布测点的问题
在测量系统已经可观察的前提下,择优增布测点即如何通过增加最少的测点来最大限度地加大测量后备重数[5]。
在测量系统不可观察的情况下,择优增布测点的出发点是如何通过增加有限个测点来最大限度地减少可观察岛的个数,扩大可观察面积,尽可能达到可观察。此时采用大节点合并拓扑法较为合适,将每个可观察岛合并成为一个大节点后,以大节点为单位寻求增加测点的方法,分析规模大大缩小,同时确定出的候选测量都是有益于扩大可观察岛范围的。
5 算例分析
5.1 可观察判断
对于图3的IEEE 14节点系统,运用第2.3节数值法与拓扑法相结合的方法进行分析。
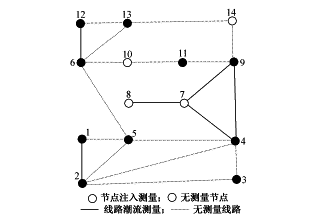
图3 IEEE 14节点模型
Fig.3 IEEE 14-bus system
经过前两步的处理(参见图4),14节点变为6节点的网络,形成H矩阵如表1所示。
经过高斯按列消元后,判断系统为可观察。
5.2 后备重数分析结果
后备重数分析结果见表2。由分析结果可见:尽管系统的16个测量中有8个测量具有二重后备,有7个测量具有一重后备,但因存在一个孤立测量7—8,系统达不到m-1级安全度。
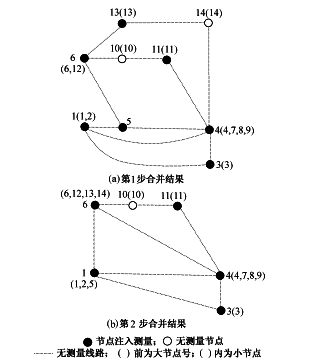
图4 第1步、第2步处理结果
Fig.4 Result of the first and second process step
表1 H矩阵
Table 1 Matrix H
节点注入测量
大节点号
1
3
4
6
10
11
小节点2
2
-1
-1
0
0
0
小节点3
-1
2
-1
0
0
0
小节点4
-1
-1
2
0
0
0
小节点5
2
0
-1
-1
0
0
小节点6
-1
0
0
2
-1
0
小节点9
0
0
2
-1
0
-1
小节点11
0
0
-1
0
-1
2
5.3 择优增布测点分析
候选测量共有18个:1—5,2—3,2—4,2—5,3—4,
表2 后备重数分析结果
Table 2 Result of meter backup analysis
序号
测量名称
后备重数
序号
测量名称
后备重数
1
[1] [2] 下一页
|


