李碧君1 薛禹胜2 顾锦汶2
1.浙江大学 310027 杭州 2.电力自动化研究院 南京 210003
0 引言
电力系统的许多领域需要进行数据处理,最小二乘法是应用最广泛的数据处理方法,对于严格服从正态分布的数据,最小二乘法估计具有方差最小且无偏的统计特性,其数学模型简洁,计算方法简单。然而,亦存在缺点,不具备处理粗差(gross error, bad data)的能力,数据中的粗差严重歪曲最小二乘法估计的结果。抗差估计(robust estimation)理论是为适应处理粗差的需要而发展起来的,已经成为一门受到较多关注的分支学科。抗差估计理论体系已经基本形成,一维参数抗差估计理论基本完善,多维参数抗差估计理论仍待进一步研究。文献[1]提出等价权的概念,将抗差估计问题转变为经典最小二乘问题,既实现了抗差估计,又保留了最小二乘法估计的许多优点。抗差估计是指在粗差不可避免的情况下,选择适当的估计方法,尽可能避免粗差的影响,得出正常模式下的未知量的最佳估计值。抗差估计的原则是充分利用有效信息,限制利用可用信息,排除有害信息。抗差估计的目标是:在假定的观测分布模型下,估计值应是最优或接近最优;假设的分布模型与实际分布模型有较小差异时,估计值受到粗差的影响较小;当假设的分布模型与实际的分布模型有较大偏离时,估计值不致受到破坏性的影响。抗差估计要求在假定的模型下,估计精度高,在模型附近,估计精度较高。
抗差估计与经典估计理论的根本区别是:抗差估计理论建立在符合数据实际分布模式的基础上,而经典估计理论建立在某种理想的分布模式基础上。将抗差估计理论应用于电力系统状态估计已取得一些理论研究成果,尤其应用于电力系统实时控制和负荷预报等领域具有重要意义。
1 抗差估计理论的重要概念
1.1 污染分布
实践证明,严格服从某一特定分布的观测数据是不存在的,污染分布表示实际分布偏离理想分布,用下式描述:
G=(1-c)F+cH
其中 F为主体分布;H为干扰分布;c为污染率。
显然,为了得到分布为G的最优估计,仅根据分布F采用极大似然估计是不够的,必须分别根据分布F和H采用相应的估计,然后根据c组合这两种估计才能得到较好的估计结果。
1.2 影响函数
影响函数描述在大子样的情况下,一个观测值对参数估计值的影响:
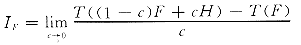
其中 T(.)为统计函数。
影响函数的一些特征,如形状、峰点、最大斜率、跳跃点、跳跃点的高度、函数值为零的一些点及这些点之间的间隔都是设计抗差估计的重要信息。基于影响函数有3种定量抗差性能的量度指标:
a.最大影响函数——量度一个固定的小污染对估计量的最坏影响,可作为估计量偏估差的上界。
b.最大影响梯度——表示一个观测值从x1移到y1对估计量的最坏影响。
c.淘汰点——当IF在某一定区域内为零时,粗差对估计量没有任何影响。影响函数不仅是设计各种不同类型抗差估计目标的依据,而且是衡量估计方法的可靠性和抗差能力的理论基础,将无穷的概念引入估计理论,把抗差原理同传统的渐近理论联系起来,是抗差估计理论走向成熟的一个重要标志。
1.3 崩溃污染率
崩溃污染率表示在不造成破坏性影响的前提下,所能容许的实际分布模式与假设分布模式的最大偏差。简言之,是指观测数据中最多存在多少粗差数据仍使估计有效。可以根据实际问题的需要选定一种表示偏离大小的指标,如用距离,或用粗差数据个数与总的观测数据个数的比值表示。崩溃污染率是估计量的抗差性的整体量度,反映了全局的抗差能力。一般而言,崩溃污染率与主体分布F及量度距离的类型无关。
1.4 抗差估计的准则
抗差估计的准则是指总体分布的参数形式给定之后,寻求最优估计方法的原则。Huber提出的极小极大准则可用来选择最优估计,它是抗差估计的统计特性方面的指标。常用的抗差估计准则有[2]:最大B—抗差估计准则、最大V—抗差估计准则、最优B—抗差估计准则和最优V—抗差估计准则。最大B—抗差估计准则就是使定位参数估计值的最大偏差最小,即最大影响函数最小;最大V—抗差是使尺度最大偏估差最小,二者皆为极小极大估计准则。在估计理论中,无偏估计以方差小者为好,并称之比方差大的无偏估计有效。最优B—抗差估计和最优V—抗差估计是在具有同等抗差能力的前提下使估计最有效,寻求估计抗差性和估计效率的统一。
1.5 杠杆观测
杠杆观测值中出现粗差,很难通过检测其自身残差的大小来发现,而有可能在其它观测的残差中有所反映,且因此可能导致错误的粗差定位。杠杆观测是观测系统结构中的弱点,与网络结构、量测配置、观测函数、权和参数的选择有关。从几何意义上讲,杠杆观测对拟合线(或超平面、体)具有很强的吸引作用,有时几乎控制了整个拟合趋势,一旦杠杆观测值中出现粗差,拟合趋势会受到严重歪曲,杠杆观测有很强的保差作用,其观测值中的粗差使估计结果严重偏离真值,因此对杠杆观测要采取适当措施加以改善。对杠杆观测的处理要慎重,既要防止杠杆观测值中出现粗差,又要增强这些观测值的精度以保持几何上的稳定性。在抗差估计理论中,削弱或消除杠杆观测的保差作用称为结构空间抗差,一个全面的抗差方案应当包括观测空间抗差和结构空间抗差。杠杆观测与电力系统状态估计中的关键量测的区别是:去掉关键量测则系统不可观测,而去掉杠杆观测不影响系统的可观测性。
2 抗差估计方法
2.1 抗差估计的类型
a. L估计:设(X1,X2,…,Xn)是分量相互独立且服从同一分布F的随机向量。把Xi(i=1,2,…,n)按其大小顺序排列,得X(1)≤X(2)≤…≤X(n),函数X(i)就是第i个排序统计量。可由此定义排序统计量的分布函数,进行排序线性组合估计,这就是L估计,它具有计算简单、直观的特点,特别适用于计算机模拟各种不同类型的抗差估计并对它们的抗差能力和效率进行检验,这也是抗差估计理论研究的一个重要组成部分。
b. R估计:设L1,L2,…,Ln都是实数,且互不相等,若在L1,L2,…,Ln中,有Ri个观测值不超过Li则称Ri为Li的秩,R={R1,R2,…,Rn}构成一个统计量,称R及由它派生的统计量为秩统计量,由秩检验导出的估计量称为秩检验型估计或R估计,属于非参数估计类型。
c. M估计:是经典极大似然估计的推广,称为广义极大似然估计。M估计在实际中应用最为广泛。对观测方程组:
L=Ax+V
式中 A是m×n阶系数矩阵;x是未知向量;L是观测向量;V是L的残差向量。
M估计的准则函数是:
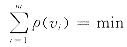
或定义M估计为下式的解:
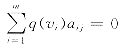
其中 ρ(.)为适当选择的凸函数;q(.)为适当选择的单调正半轴非降函数;vi为残差;aij为系数阵A的第i行第j列元素。
有一个ρ(*)(或q(*))函数就定义了一个M估计,因此这里定义的M估计实际上是一类估计。设计M估计实际上是根据具体问题的需要建立函数ρ(.)或q(.)。经典最小二乘法估计是一种特殊的M估计,它不具有抗差能力。常用于抗差估计的M估计有:中位数估计,Tukey双权估计,Huber估计等。它们各有优缺点,中位数估计方法的抗差能力最强。根据文献[1]提出的等价权的思想可以求出它们的等价权,从而将抗差估计问题转变为抗差最小二乘法估计问题,以便充分利用最小二乘法估计的一些研究成果。
2.2 常用估计方案的ρ(.),q(.)函数和等价权因子w(.)
2.2.1 最小二乘法
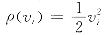
q(vi)=vi
w(vi)=1
其中 vi=(li-aix)/σ;σ2=(L-Ax)T(L-Ax)/(m-n);ai为系数阵A的行向量。
2.2.2 中位数或L1估计
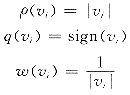
其中 vi=(li-aix)/KMAD;KMAD=medi|li-aix|。
绝对和极小法为中位数估计的一种。
2.2.3 Tukey双权法
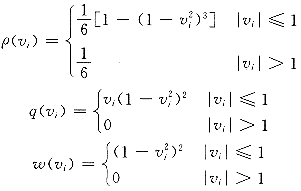
其中 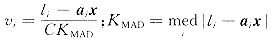 ;C为回归因子。 ;C为回归因子。
2.2.4 Huber法
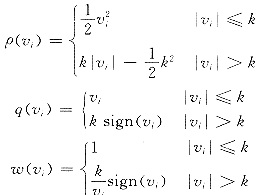
其中 vi=(li-aix)/s;s在|vi|≤k区间取标准差,在|vi|>k区间取KMAD。
3 抗差估计理论在电力系统中的应用
3.1 抗差估计理论在电力系统状态估计中的应用
电力系统状态估计应用最多的是加权最小二乘法(WLS)估计,它有经典最小二乘法估计方法的所有优良统计特性,但它的估计结果对量测中的粗差(坏数据)十分敏感,当量测粗差不能全部被剔除时,估计值将严重偏离真值。应用抗差估计理论,能大大减小粗差数据对估计结果的不良影响,有望在削弱粗差数据对估计结果的不良影响,提高估计精度方面取得较大进展,国外已有一些学者在进行这方面的研究,并取得了一定的成果。
Merill和Schweppe早在1971年就提出用Non-Quadratic估计器抑制坏数据,Handschine等人对多种Non-Quadratic估计器和坏数据的检测和辨识进行了深入研究,Irving等人首先提出用线性规划求解最小绝对值(LAV)估计问题[3],国外学者研究过的抗差估计器还有其它中位数(least median of squares,缩写为LMS)估计器[4]。因为抗差估计与WLS估计相比具有模型复杂和计算量大等特点,受当时计算机技术的限制,难以实用,所以长时间未受到特别关注。随着计算机技术的迅猛发展,国外许多学者对抗差估计理论应用于电力系统状态估计表示出了极其浓厚的兴趣,美国自然科学基金也在资助这方面的研究课题。
Mehmet等人认为杠杆点(leverage point)是影响加权最小绝对值(WLAV)估计抗差性的主要原因,对杠杆点的处理方法有:在估计前辨识和消除杠杆点坏数据,开发对杠杆点不敏感的估计方法,如文献[5]提出用线性变换量测方程坐标系的方法,改变量测雅可比矩阵的结构,从而消除原量测集中的杠杆点,然后再用WLAV估计,在有多相关坏数据时仍有好的估计性能。Clements等人在文献[6]中综合考虑随机量测误差和随机量测仪表故障,量测仪表工作正常时,量测服从正态分布,概率是α,量测仪表工作不正常时,量测不再服从正态分布,概率是1-α,在此基础上导出了两种估计器QL(quadratic-linear)和QC(quadratic-constant),QL估计与Huber估计密切相关,QL估计和QC估计的计算量是WLS估计不排除坏数据时计算量的两倍,但能得到较精确的估计结果。QC估计比QL估计有更好的抗差能力,因为QC估计考虑了量测仪表工作的自然特性。作者正在研究比较各种Non-Quadratic估计算法和尽力提高估计计算速度。LMS估计是崩溃污染率最高的估计方法,在杠杆量测有坏数据时仍能保持抗差性,能够处理最多的坏数据[7],Mili和Rousseeuw等人对LMS估计和LTS(least trimmed squares)估计进行了研究[7,8],指出LMS估计能辨识坏数据的最大数目由系统冗余量测数目决定,提出将系统分解成若干个子系统,分别用LMS估计或LTS估计辨识坏数据,从而提高全系统辨识坏数据的能力。他们还应用多元统计学理论辨识杠杆量测,在G—M估计(general M estimator)中对含粗差和不含粗差的杠杆量测区别对待,用等价加权最小二乘法求解,只需对WLS估计作简单修改,计算速度比较快[9]。
抗差估计理论应用于电力系统状态估计在以下方面还有待进一步深入研究:
a.加快抗差估计算法的速度。这是抗差估计器能够实时应用的关键,不同电力系统的量测,同一电力系统的不同量测,同一量测在不同时段的分布模式都不尽相同,实时辨识量测量的分布特性,使用相应的抗差估计器,提高估计精度。
b.含参数错误和网络拓扑错误的抗差估计研究。
c.量测相关的抗差估计研究。
d.有偏抗差估计等。
3.2 抗差估计理论在电力系统实时控制和负荷预报等领域中的应用
通常与时间密切联系的动态随机模型有两类[1]:一类是离散时间状态系统,另一类是时间序列系统。电力系统实时控制和负荷预报等领域也是这两类动态随机模型,对它们的应用已有深入研究。一般都是假设观测误差是白噪声,实际上,观测量被粗差污染的情况并不罕见,观测误差是广义白噪声,某些待估参数的先验信息可能被有害信息污染,沿用原有的估计理论和方法,有时得到的估计结果会偏离真值很远,甚至导致不良后果。针对这种复杂情形,用抗差估计的方法,可望得到可靠、真实的估计结果。在电力系统实时控制中,离散系统的状态估计模型采用抗差估计理论设计抗差滤波器;在负荷预报的时间序列分析中,用抗差估计理论作粗差探测,排除历史负荷数据中不能反映真实负荷规律性的那些数据,由此预计未来的负荷,有望提高状态模型参数估计辨识的精度和负荷预报的准确度。目前还未看到有关这方面的文献,值得关注。
4 结语
实际观测数据并不严格服从正态分布,观测数据中难免出现一定的粗差数据,此时应用经典最小二乘法估计会使估计结果严重偏离真值,基于最小二乘估计的坏数据的检测与辨识方法还没有完善。抗差估计理论是为适应处理粗差的需要而发展起来的,已经发展成为一门受到较多关注的分支学科。电力系统的许多领域需要对观测数据进行处理,抗差估计理论可望在电力系统的很多领域中得到应用,因而具有重要的应用研究价值
|


