|
1引言
近年来,随着控制理论的不断完善,控制系统的故障诊断方面的研究越来越引起了人们的重视[1][2],并且相继取得了很多研究成果[3][4][7]。然而,正如文献1中所提到,动态系统的故障诊断技术,目前取得的成果主要集中在线性系统上,而针对非线性系统的研究则鲜见于文献。更为重要的是,由于理论研究中对模型所做的假设在实际应用中经常得不到满足,因此给故障诊断技术的实际应用带来了巨大的困难。文献7从理论上对这种应用难度进行了探讨和归纳,对基于模型(尤其是通过观测器来进行)的故障诊断方法的设计方向和性能评价提供了有意义的指导。由于应用上的难度和电力电子本身存在的非线性等因素,电力电子作为现代控制中的重要技术手段,对其进行故障诊断方面的研究却迟迟没有进行。本文从理论和实际应用的角度出发,先对电力电子系统的故障进行了分析,然后针对具体的某一类故障,设计出一种基于模型的故障诊断方法。仿真结果表明,文中提出的方法是行之有效的。
2电力电子系统的故障分析
电力电子系统中故障的来源是多方面的,下面以一个常用的电压反馈型逆变器控制系统为例来分析主要故障。
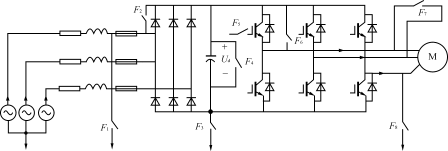
图1电力电子控制系统的常见故障
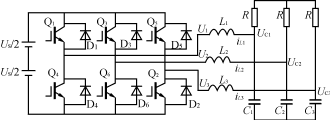
图2三相逆变器
图1中列出了这个电力电子控制系统中通常可能出现的8种故障Fi(i=1,2,…,8),其中除F5故障用开关断开表示外,其它故障用开关闭合来表示。这些故障是:
F1输入电压单相接地故障;
F2整流二极管短路故障;
F3直流接地故障;
F4直流滤波电容短路故障;
F5GTR基极开路故障(无驱动信号);
F6GTR短路故障;
F7电动机线间短路故障;
F8电动机单相接地故障。
上面列出的故障没有考虑电机内部的故障。事实上,在电力电子装置的实际设计中会加上许多保护电路,如短路保护,过电流/电压保护等。然而,从容错控制和保护器件的角度出发,系统对这些故障进行检测和分离是十分有意义的研究工作。文献6中对其中最为重要的四种故障(F1、F2、F5、F6)在电路理论上进行了分析,但其分析只是概述性的,还有更多具体的工作需要进一步的研究。例如,如果GTR出现单臂基极开路故障,系统是能够继续降性能运行的,此时由于相电压中产生很大的直流分量,在电机上将产生直流脉动转矩,对系统是有害的,因此要及时分离出故障臂,排除故障。
3三相逆变器的故障诊断
31三相逆变器的Kalman模型
三相逆变器在正常工作时,其电路结构如图2所示。
图中Qi(i=1,2,3,4,5,6)是开关器件,电阻R为负载,电感L、电容C组成滤波电路(这样的负载在UPS中很常用),Us为直流侧的供电电源,在图1中为滤波电容两端电压Ud。
取电路中uc1,uc2,uc3,iL1,iL2,iL3作为状态量,U1,U2,U3作为控制量,iL1,iL2,iL3作为输出量,则系统可采用下面的Kalman模型进行描述:
x=Ax+Bu
y=Cx
式中:x∈R6,u∈R3,y∈R3,
A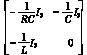 =∈R6×6, =∈R6×6,
B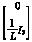 =∈R6×3, =∈R6×3,
C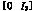 =∈R3×6,I3∈R3×3 =∈R3×6,I3∈R3×3
32三相逆变器的故障模型
对于上述逆变器,根据前面的讨论可知,它可能发生的故障主要是F5或F6。其中当出现F6时,由于会立即出现电源间短路,保护电路会迅速起动,关闭系统的运行,因此对其进行故障检测和分离的意义不大。下面我们针对F5进行分析。
当逆变器某一个晶体管出现基极开路故障时(以Q3为例),负载电流将不再为正弦波形。如果此时相电流iL2>0,则iL2无法连接到电源的正端,而只能够通过Q6的旁路二极管连接到电源的负端,从而iL2迅速衰减到0。在这个过程中,电流控制器的输出要增大以补偿iL2的衰减。当电流回到负半周时,Q3不再起作用,系统正常工作。这样,从整个运行周期来看,故障相电流将在负载上产生直流分量,对系统运行是有害的,应该排除故障。设逆变器各相产生的PWM控制电压为ui=Vi(i=1,2,3),则当某相上臂GTR出现基极开路故障时,该相控制电压变为: 而当其中一相下臂GTR出现基极开路故障时,该相控制电压为: 而当其中一相下臂GTR出现基极开路故障时,该相控制电压为: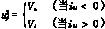 因此,系统在故障情形下,状态方程为: 因此,系统在故障情形下,状态方程为: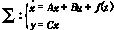 其中fi(t)(i=1,2,…,k,k=6)表示Qi基极开路时的故障向量见式(6): 其中fi(t)(i=1,2,…,k,k=6)表示Qi基极开路时的故障向量见式(6):
对于由式(4)(5)组成的系统Σ,我们有如下定义和定理。
定义1对于系统Σ,当它只发生单故障时,如果对于ik,jk,i≠j,fi(t)引起的系统响应Yi(t)与fj(t)引起的系统响应Yj(t)不相同,即Yi(t)≠Yj(t),则称故障向量fi(t)和故障向量fj(t)是可区分的。如果任意两个向量是可区分的,则称系统为单故障源可隔离的。
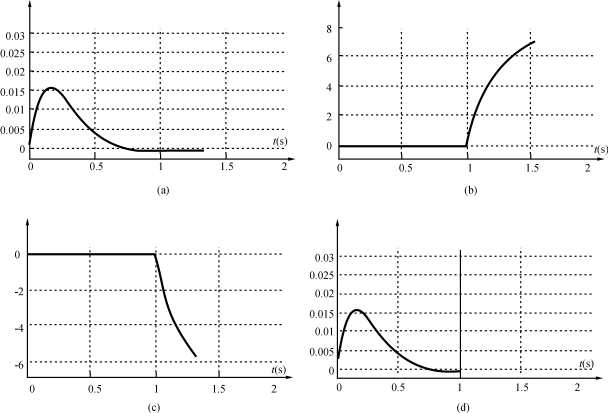
图3系统运行时正常与故障相电流观测误差
(a)系统运行时未出故障相电流的观测误差(b)Q1、Q3或Q5出现基极开路故障时对应相电流观测误差
(c)Q4、Q6或Q2出现基极开路故障时对应相电流观测误差(d)Q1、Q3或Q5出现基极开路故障时对应相电流观测误差(精度放大)
定理1对于系统Σ,如果是由一组方程式(6)来描述的故障向量,则Σ是单故障可隔离的。
证明:对一组方程式(6)所描述的向量,显然对于任意ik,jk,i≠j,(k=6),由于fi(t)≠fj(t),因此各自引起的系统响应有Yi(t)≠Yj(t),所以根据定义1可知Σ是单故障可隔离的。
33故障观测器的设计
对于故障系统Σ,我们采用如下形式的标准Luenberger观测器。   =A+Bu+D(y-) =A+Bu+D(y-)  =A+Bu+D(Cx-C) =A+Bu+D(Cx-C)  则可以得到:ex(t)=(A-DC)ex+fi(t),ey=Cex,其中ex=x-,ey=y-。我们设计的目标是选择合适的矩阵D使得A-DC为稳定矩阵。设D=[D1D2}T,D1,D2∈R3×3则: 则可以得到:ex(t)=(A-DC)ex+fi(t),ey=Cex,其中ex=x-,ey=y-。我们设计的目标是选择合适的矩阵D使得A-DC为稳定矩阵。设D=[D1D2}T,D1,D2∈R3×3则: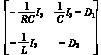 A-DC=(8) A-DC=(8)
从式(8)可以看出,如果我们取D1=I3,D2=dI3(d>0),则观测器是收敛的。从而得到误差方程的解为: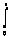 ex(t)=e(A-DC)ex(0)+e(A-DC)(t-τ)fi(τ)dτ ex(t)=e(A-DC)ex(0)+e(A-DC)(t-τ)fi(τ)dτ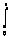 →e(A-DC)(t-τ)fi(τ)dτ(9) →e(A-DC)(t-τ)fi(τ)dτ(9)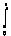 ey(t)=Ce(A-DC)ex(0)+Ce(A-DC)(t-τ)fi(τ)dτ ey(t)=Ce(A-DC)ex(0)+Ce(A-DC)(t-τ)fi(τ)dτ →Ce(A-DC)(t-τ)fi(τ)dτ(10) →Ce(A-DC)(t-τ)fi(τ)dτ(10)

所以,如果fi(t)=0,ex(t)→0,ey(t)→0;如果fi(t)≠0,则根据定理1,我们可以从输出的观测误差中检测并分离出故障,明确定位出发生基极开路故障的GTR。
4仿真结果
从下面的仿真结果可以看出,系统在无故障情况下,各相电流观测误差均能够快速收敛到0。即使某一相发生F5型故障,其他无故障相电流观测误差仍然不受影响地收敛到0〔图3(a)〕。图3(b)、图3(c)和图3(d)中在1s时刻发生故障,从中可见,当某一相的GTR出现基极开路故障时,其对应相电流观测误差将迅速发生突变,且突变方向表示了上臂GTR故障和下臂GTR故障之间的不同,因此可以用来准确确定故障源。
5结语
尽管控制系统的故障诊断技术在各方面取得了进展,但其在电力电子系统方面的应用研究却不多见,这与电力电子技术被广泛应用的现状是不协调的。由于电力电子器件的数学模型在研究运动系统控制的同时已经得到了比较深入的研究,因此将已有的、理论和实践上都比较成熟的故障诊断技术,应用到电力电子方面的故障诊断中,必定会取得令人满意的结果,也必定是件很有意义的工作。由于电力电子系统故障必然会导致系统状态与输出量中各基波量和谐波量的变化,因此,如果采用基于信息处理的故障诊断方法来进行这方面的故障诊断,这也是现在尚未开展但又可行而有意义的研究方向。本文采用的基于观测器的故障诊断方法,从理论分析和仿真结果来看,都不失为一种行之有效且实现简单的方法,可以直接结合到控制系统中进行应用。
|


