|
本文提出了一种基于粗糙集理论的电力变压器绝缘故障诊断新方法,它能够根据不完整征兆信息对电力变压器故障进行诊断。该方法不但可直接从完备的故障征兆样本集中导出正确的诊断结论,而且还能从不完备的故障征兆样本集中导出满意的诊断结论,它揭示了故障征兆信息的冗余性。实例诊断结果证实了该方法的有效性。
关键词:粗糙集;决策表;故障诊断;电力变压器
Diagnosis of Insulation Malfunction in Power Transformer Based on Rough Set Theory
Wang Shao-fang, Cai Jin-ding, Liu Qing-zhen
( Dept.of E.E,Fuzhou University Fuzhou 350002)
Abstract: In this paper,a new method applied for identifying power transformer insulation malfunction based on rough set theory is proposed,which can identify power transformer malfunction based on incomplete symptom information.The accurate diagnosis results can be obtained directly from the set of complete fault samples,and the satisfactory diagnosis results can also be got from the set of incomplete fault samples by using the approach.The inherent redundancy in the fault information is revealed.The validity of the approach has been verified by the diagnosis rerults of practical examples.
Key words:Rough Set,Decision table,Faulte diagnosis, Power Transformer
0 引言
随着电力系统朝着超高压、大容量的方向发展,对电力设备运行可靠性的要求不断提高。如大型电力变压器作为电力系统中重要的变电设备,其运行状态将直接影响到电力系统的安全运行。所以,如能迅速而准确地对其进行故障诊断,防患于未然,将是保障供电可靠性的重要手段之一。
电力变压器的故障实质上是一个模式分类问题,即根据各种各样的故障征兆,判断出故障发生的部位或区域。由于电力变压器故障征兆与故障原因之间存在着很多不确定因素,所以一种故障可能会引起多个征兆,而一种征兆又可能由几种故障引起。本文用粗糙集理论,考虑故障征兆信息的不准确、不完备性,提出一种电力变压器常见绝缘故障的诊断模型。
1 粗糙集理论
粗糙集理论(Rough Set Theory, RST)是Pawlak Z.及其合作者于1982年提出的一种处理模糊性和不精确问题的新型数学工具[1,2]。它的最大特点是不需要提供求解问题时所需处理的数据集合之外的任何先验信息,如统计中要求的先验概率和模糊集中要求的隶属度,即能有效地分析和处理不精确、不一致、不完整等各种不完备数据,并从中发现隐含的知识,揭示潜在的规律[3]。
1.1 粗糙集的上、下近似集[3]
在RST中,用等价关系代替分类,设U≠Φ是论域,R为U上的一族等价关系,二元对K=(U,R)构成一个近似空间(Approximation space)。R将论域U分成一族等价类Ei(i=1,…,n),Ei和空集Φ 称为R的基本集。如果U上的一个子集X不能用基本集的并集准确表示出来,则称X为粗糙集,粗糙集是用上近似集和下近似集两个精确集来描述的,其数学定义如下:
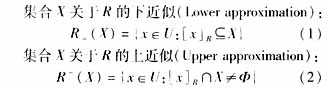
其中x为U中的一个对象,[x]R表示所有与x不可分辨的对象组成的集合,即由x决定的等价类。实际上R_(X)是U中包含在X中的最大可定义集,R-(X)是U中包含在X中的最小可定义集。
1.2 决策表[4]
信息系统IS(Information System)可表示为IS=〈U,A,Va,fa〉,其中U是对象的非空有限集合,称为论域;A是对象属性的非空有限集合,称为属性集合;Va=∪a∈AVaa是属性值的集合,Vaa表示属性a∈A的值域;f:U×A→Va称为信息函数。信息系统也称为知识表达系统.由这样的“属性—值”对就构成了一张二维表,称之为信息表(Information table)。
如果A由条件属性C和结论属性D组成,且C,D满足:
C∪D=A, C∩D=ø
则称IS为决策系统(Decision System,简称DS)。
实际使用时,决策系统一般表示成一张决策表(Decsion table)的形式,每一列表示一个属性,每一行表示一个对象。
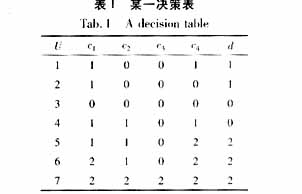
例1:假设一个由7个对象的简单决策系统,有4个条件属性c1,c2,c3,c4,一个决策属性d,如表1所示:
1.3 决策表的化简及分类规则的提取
决策表中的一个属性对应一个等价关系,一个决策表可看作是定义的一族等价关系。决策表中并非所有的条件属性都是必要的,有些是多余的,去除这些属性不会影响原有的表达效果。决策表的化简就是化简表中多余的条件属性,即去除冗余的条件属性,在删除这些属性后不会影响原有的表达效果,化简后的决策表具有更少的条件属性但具有化简前的决策表的功能。
决策表的简化步骤如下:
(1) 删除条件属性集合的冗余属性,找到所有约简。首先定义决策规则的协调性:相同的规则前代(即属性部)必然有相同的后继(即结论部);不同的规则前代允许有不同或者相同的后继;相同的后继允许相同或不同的前代。判断某一个条件属性冗余或可省的准则是:若去掉条件属性集中某属性后,算法中所有规则仍然协调,则该属性冗余而可省去;若有一个规则不协调,则该属性不可省。同理,依次单独去掉其他条件属性来考察规则的协调与否,去掉所有冗余条件属性。例如逐一除去表1中条件属性c1,c2,c3,c4,看看没有该列决策表是否协调。检查后发现c3是多余的,而c1,c2,c4是必需的属性。{c1,c2,c4}称为原条件属性集{c1,c2,c3,c4}的一约简。一个决策表的条件属性集可能存在多个约简。本例中只有一个,见表2。
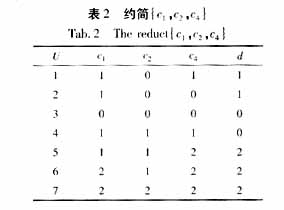
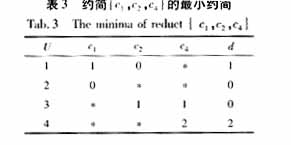
(2) 对每个约简进一步化简,找到最小约简。假设每个约简有L个决策规则,R个条件属性,那么先删除第i个决策规则的第j个条件属性aij,然后将该决策规则剩余的R-1个条件属性ain(n=1-R,n≠j)与其余L-1个决策规则的对应条件属性amn(m=1~L,m≠i)进行比较,若条件属性完全相同则再看决策属性是否相同,相同则表示该被删除的条件属性aij是冗余的,反之则不是冗余的,依此类推以实现最小约简。对于表2化简后得到的最终决策表见表3,符号 *表示该属性的取值对分类没有影响。显然,表3比表1要简单得多,它仅包含了那些在决策时所必需的条件属性值,但它具有原始知识系统的所有知识和分类能力。

2 基于粗糙集理论的变压器故障诊断
变压器的故障诊断可描述成一个模式分类问题,因此很适合用粗糙集理论的决策表方法来处理,其基本思想是把观察或测量到的变压器故障征兆作为对故障分类的条件属性,实际存在的故障作为决策属性建立决策表,先利用粗糙集理论强大的约简能力对原始信息进行化简而得到多个与原始信息表等价的约简,然后对约简进一步化简,找到最小约简,并抽取决策规则。根据实际某台电力变压器的故障征兆,找到对应的规则,就能对其进行诊断。实际上,它是利用故障信息的冗余性,通过避开遗漏的或错误的信息来处理不完备的故障信息。
表4给出了征兆集合M列表,表5给出了故障类型及其相应的征兆[5],根据表5就可以写出电力变压器故障诊断的决策表(见表6)。在表6中U表示样本编号,mi(i=1,2, …, 11) 和D分别表示条件属性和决策属性。其中条件属性mi的值1表示该征兆信息出现或不正常,0表示不出现或正常。


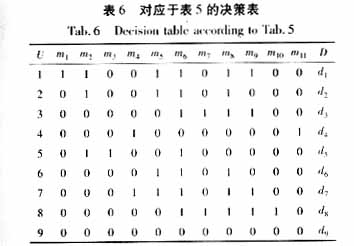

中约简{m2,m4,m8,m9,m10}如表7所示。这11个约简保持了与原决策表完全相同的分类能力,但所需的条件属性却大大减少,对以上11个约简进一步消去每一决策规则的冗余属性,可得最小约简,其中约简{m2,m4,m8,m9,m10}的最小约简如表8所示。决策表的最小约简清晰地显示了每个故障的重要特征,它们具有与原决策表相同的诊断能力。
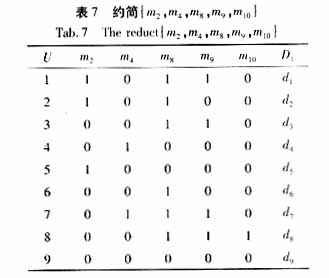
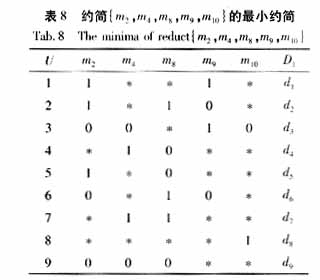
表中*表示取'0'或'1'
从表8中可提取9条简化的故障诊断规则,如规则1(Rule1):if( m2=1 and m9=1) Then(D=d1) ,规则2(Rule2):if( m2=1 and m8=1 and m9=0) Then(D=d2) 等。利用这些简化的诊断规则可以很容易地对电力变压器的故障进行诊断。
对表8中的9条判断变压器故障类型的规则进行测试可以看到:(a)若故障的征兆完备,它们能准确地区别这9种类型的故障;(b)若遗漏的或错误的信息不是约简中的关键信息,对分类结果无影响;(c)若遗漏了关键信息,可选择不同的约简,通过避开遗漏的关键属性,利用多数判决的原则进行综合诊断。
3 故障诊断实例
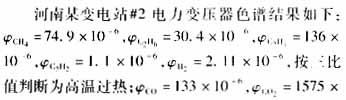
10-6,则有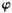 co/ co/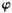 co2=0.084,其值小于0.09,似为异常;在电气实验数据中,又给出了三相不平衡系数,其值大于2%,不正常;局部放电量100pC,合格[5]。由表8中提取的规则: co2=0.084,其值小于0.09,似为异常;在电气实验数据中,又给出了三相不平衡系数,其值大于2%,不正常;局部放电量100pC,合格[5]。由表8中提取的规则:
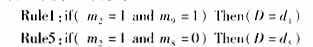
判断故障为铁心多点接地及局部短路和分接开关事故及引线故障两种故障。实际吊芯检查结果为铁芯接地铜片过长,搭接了铁轭部分硅钢片,从而造成铁心局部短路;同时有载分接开关的操作杆下端槽口有烧黑痕迹。可见诊断结果与实际情况相符合。
4 小结
(1)由于RS理论在处理不精确问题时,不需要提供求解问题所需处理的数据集合之外的任何先验信息,且能够在保留关键信息的前提下对数据进行化简并求得知识的最小表达,能够处理含有遗漏或错误信息,适合于变压器故障诊断,能够处理变压器的复合故障。
(2)把电力变压器的故障征兆作为对故障分类的条件属性集,以决策表为主要工具,利用决策表的约简形式,抽取出诊断规则,就能实现电力变压器的故障诊断。该方法不但可直接从完备的故障征兆样本集中导出正确的诊断结论,而且还能从不完备的故障征兆样本集中导出满意的诊断结论,它揭示了故障征兆信息的冗余性。实例诊断结果表明了该方法不但能处理压器的复合故障,而且能初步确定故障的部位。
|


