袁荣湘1 陈德树1 马天皓 张哲1 尹项根1
1.华中理工大学电力系,湖北 武汉 430074 2.中兴通讯公司监控产品部,广东 深圳 518004
常规的电流差动保护中差动量和制动量的求取一般是反应电流的有效值或平均值等,通过滤波等办法消除非周期分量和谐波分量的影响。在计算机继电保护的有效值计算方法中,故障时引起的非周期分量和谐波分量尽管衰减很快,但可能在较长时间内影响计算的准确性,即采用时间窗为一个周期的算法,若开始几个采样值中含较高的非基波分量,则将影响与这些采样值相关的各个周期的计算结果。如果要保证保护动作的可靠性,势必影响保护的动作速度。若电流差动保护的动作判据按每一个采样值分别判断,则可以在原理上完全消除这种影响,有效地提高电流差动保护的动作速度与可靠性。正是基于这些方面的考虑,参考文献[1]讨论了采样值电流差动保护的有关问题,本篇将在此基础上对采样值电流差动保护与常规电流差动保护的关系和它们的动作边界变化区作进一步的研究。
1 电流差动保护的传统方法
电流差动保护适用任何数量支路的条件,其判据亦有很多种,但不论是哪一种判据,其基本部分(动作量)总是以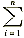 Ii为基础的,其中Ii为任一支路的电流(规定母线流向线路为电流正方向),n为线路数。各种判据的区别在于附加的制动项构成的方法不同,但它们都是各线路电流的函数,可简单将其归并为两端电流,分别以Im,In表示。这样可归纳出传统电流差动保护常见的动作判据有以下几种形式: Ii为基础的,其中Ii为任一支路的电流(规定母线流向线路为电流正方向),n为线路数。各种判据的区别在于附加的制动项构成的方法不同,但它们都是各线路电流的函数,可简单将其归并为两端电流,分别以Im,In表示。这样可归纳出传统电流差动保护常见的动作判据有以下几种形式:
|Im+In|≥I0;|Im+In|≥K1(Im+In);
|Im+In|≥K2max(Im,In);|Im+In|≥K3|Im-In|;
|Im+In|2≥-K4ImIncos
Im,In为两端电流向量;Im,In为两端电流向量的幅值;I0为整定的动作门槛值;K1~K4为整定系数; 为两端电流向量的夹角。 为两端电流向量的夹角。
对电流差动保护的分析方法可采用以两端电流Im,In的关系表示。这类分析中有两种常见的方法:比率差动特性法是在线路两端电流相位相差180°的条件下作出的,主要适于分析在外部故障时保护的动作行为;相位特性法是在线路两端电流大小相等的条件下作出的,适于分析在线路两端电流大小相等时保护在内部和外部故障时的动作行为。对电流差动保护的分析也可以用差动电流和制动电流的关系表示,通常称为制动特性。传统电流差动保护性能的分析可参见文献[2],在此不赘述。
2 采样值电流差动保护与常规电流差动保护的关系
采样值电流差动保护利用电流采样的瞬时值来实现基于相量的常规电流差动保护动作判据。假设故障时采样的电流仅由基波分量构成,即已滤去谐波分量、非周期分量等非工频成分,则前面的各种判据一般可简化为如下两种形式或这两种形式的组合,即
|A|>|B| (1)
或
|A|>C (C为常数) (2)
先考虑(1)式,对应的采样值电流差动保护判据为
|Asinθ|>|Bsin(θ-Δθ)| (3)
式中 A对应于Asinθ;B对应于Bsin(θ-Δθ);θ为变量;Δθ为两相量A和B之间的角差;A,B分别为A,B的幅值。由于两相量角差可用区间[0,π]表示,故不妨设Δθ∈[0,π]。
当Δθ=0或π时,若(1)式成立,则(3)式恒成立;当0<Δθ<π时,不妨先设A=B,则(3)式判据变为
|sinθ|>|sin(θ-Δθ)| (4)
当Δθ≤θ≤π时,(4)式成为sinθ>sin(θ-Δθ),亦即2sin(Δθ/2)cos(θ-Δθ/2)>0。
由于sin(Δθ/2)>0,则上式等价于cos(θ-Δθ/
2)>0,即Δθ<θ<(Δθ+π)/2。
当π≤θ≤π+Δθ时,(4)式成为-sinθ>sin(θ-Δθ),亦即2cos(Δθ/2)sin(θ-Δθ/2)<0。
由于cos(Δθ/2)>0,则(4)式等价于sin(θ-Δθ/2)<0,即π+Δθ/2<θ<π+Δθ。
综上可知,θ在(π+Δθ)/2<θ<π+Δθ/2的范围内不满足(4)式,其范围大小为π/2,如图1(a)所示,动作函数与制动函数1比较为此时的最不利情形,即动作量与制动量的相位相差90°。

图1 采样值与常规电流差动保护关系示意图
现讨论当A,B不相等时,由于A>B,故θ不满足(1)式的范围将小于π/2,图1(a)中的动作函数与制动函数2比较为此种条件下的最不利情形示意图,θ不满足(1)式的范围为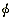 ,小于π/2。 ,小于π/2。
对(2)式,对应的采样值电流差动保护判据为
|Asinθ|>C (5)
式中 A对应于Asinθ,θ为变量。
当C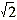 时,θ亦在小于π/2范围内,不满足(5)式,动作函数与制动函数C的比较如图1(b)所示。 时,θ亦在小于π/2范围内,不满足(5)式,动作函数与制动函数C的比较如图1(b)所示。
因此,如果不考虑非基波分量的影响和抗干扰性能时,对于采样值电流差动保护,理论上只要在半个周期中有>90°的角度范围满足其判别方程,制动效果则与其所对应的常规电流差动保护判据的制动效果相当。
3 保护动作边界变化范围的确定
采样值电流差动保护动作判据方程在>90°的角度范围内成立,对于每周期采样12个点的数字式继电保护装置来说,相当于在半个周期内有4点以上满足保护动作判据。采样初始时刻的随机性,使得采样值差动保护的动作边界并不固定。实际上,数字式保护都可能存在类似的问题,只是我们将其影响归结为求相量时的误差,而在分析保护性能时假设所求相量是绝对精确的,故没有保护动作区边界变化一说。即当采用傅氏算法、曲线拟合法等与采样初始时刻无关的算法时,当然无变化的动作边界;当采用最大值算法、半周积分法、导数算法等受采样值初始时刻变化影响的算法,则存在一定的动作边界变化区域,而且,采样值电流差动保护受采样初始时刻随机性的影响最大。采样值电流差动保护的动作区边界变化范围不会因为加长数据窗、使出口动作速度变慢而减少,仅与采样频率有关。
仍以每周期采样12个点的计算机继电保护装置为例,对于(2)式判据,如图2(a)所示,图中动作函数1与制动函数的比较表示最有利的情形,即动作函数峰值附近的两连续采样值相等,此时动作函数峰值是制动量C的2倍,图中动作函数2与制动函数的比较表示最不利的情形,即有一采样点正好是动作函数峰值,此时动作函数峰值是制动量C的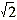 倍,对应于(2)式判据的动作区边界变化范围是:A∈( 倍,对应于(2)式判据的动作区边界变化范围是:A∈(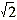 C,2C)。 C,2C)。
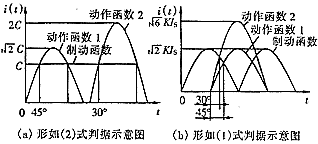
图2 保护动作边界变化范围计算示意图
对于(1)式判据,如图2(b)所示,图中动作函数1与制动函数的比较为最有利的情形,即动作函数峰值附近的两连续采样值相等,此时动作函数峰值与制动函数峰值相等,图中动作函数2与制动函数的比较表示最不利的情形,即有一采样点正好是动作函数峰值,此时动作函数峰值是制动函数峰值的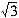 倍,则对应于(1)式判据的动作区边界变化范围是:A/B∈(K, 倍,则对应于(1)式判据的动作区边界变化范围是:A/B∈(K,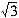 K),K为保护判据中的比例系数。 K),K为保护判据中的比例系数。
上述采样值差动保护的动作边界变化区域可在比率制动特性平面上清楚表示,如图3所示,其横坐标为制动量的幅值,纵坐标为差动量的幅值。动作区和制动区之间的区域为不定部分。图3(b)不定部分中角度为θ=arctan(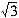 -1)K/(1+ -1)K/(1+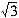 K2)。 K2)。
当保护装置每周期采样点数为N时,推而广之可以得到采样值电流差动保护动作边界的变化范围。对于(2)式的动作区,边界变化范围是:
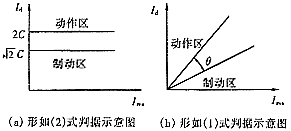
图3 采样值电流差动保护动作边界变化范围示意图
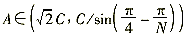
对于(1)式,其动作边界变化范围是:
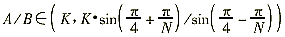
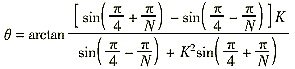
由上式可以知道,提高保护装置的采样率可以减少保护动作区边界的不定区域范围,其极限是N→∞时,这种不确定区域消失。
4 采样值电流差动保护的动作速度
使用采样值电流差动保护的重要原因之一是试图提高电流差动保护的动作速度。从上面的分析知道,保护在一个与半个周期左右动作出口,对采样值电流差动保护来说,性能没有多少区别,而由于动作边界存在不确定部分,过分提高采样值电流差动保护的动作速度则是不现实的。同时,在分析中采样值电流差动保护与传统电流差动保护制动效果相当的假设条件是,必须在半个周期中有>90°的角度范围满足动作判别方程。因此,尽管通过提高电流差动保护的采样速度,可大大减少采样值电流差动保护动作边界的变化范围,但是,采样值电流差动保护出口动作速度无论如何必须>5 ms(对于频率为50 Hz的电网来说即对应于90°),才能保证采样值电流差动保护的可靠性。
5 结论
a. 对于每周采样12点的采样值电流差动保护来说,在半个周期内满足保护动作判据的判断次数不宜小于4次(即保证在>90°的角度范围内满足动作判据),6取4的保护方案是可行的。
b. 在计算机继电保护的软、硬件条件许可下,提高数据采样率对采样值电流差动保护性能提高十分有利。提高采样率可以减少采样值电流差动保护动作边界的变化区域,同时当保护动作出口速度不变时,提高采样率将有助于改善采样值电流差动保护的可靠性。但应注意的是,不能因为采样率提高而将保护动作速度无限制地提高,原理上采样率与动作速度没有直接关系,采样值电流差动保护的出口速度极限为5 ms(对频率为50 Hz的电网而言)。
c. 如果采样值电流差动保护能保证其制动效果与常规电流差动保护的制动效果相当,那么其整定方法容易从使用相同原理判据的常规电流差动保护的整定方法中类比过来,抗电流互感器饱和的方法亦可采用常规电流差动保护中使用的同类方法。■
|


