| 由机电之家行业门户网运行 |
|
|
||||||
|
|
||||||
|
|
 |
|
| 您现在的位置： 设备维修与管理 >> 设备管理 >> 基础管理 >> 维修管理 >> 资讯正文 |
|
设 备 管 理 网 s b g l . j d z j . c o m
|
|
服务热线：0571-87774297 传真：0571-87774298 电子邮件：donemi@hz.cn 服务 QQ:66821730
机电之家(www.jdzj.com)旗下网站 杭州滨兴科技有限公司提供技术支持
|
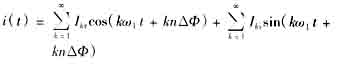移相到第1路采样时刻的各次谐波电流向量的实部和虚部按下式计算
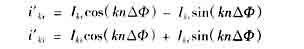其中cos(knΔΦ)和sin(knΔΦ)为已知，可以离线计算出。
用离散傅立叶变换DFT（FFT）计算电量时，利用DFT的共轭对称性，通过计算一个N点的DFT，一次可以完成两个实序列的N点DFT变换
经过幅度修正后，各次谐波的电压和电流向量为
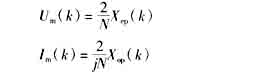如果电压先采样，电流后采样，两路采样时刻相差Δt，对应的角度为Δφ，则对基波及各谐波电流进行移相
根据非正弦周期信号的理论及以上计算结果可得
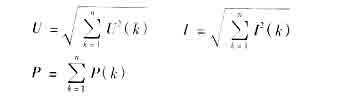非正弦周期电量无功功率的计算情况比较复杂［５］，近似用
3仿真计算及分析
仿真计算的电压、电流为含有谐波分量的函数：
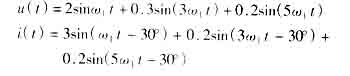对电压、电流进行顺序采样，每个工频周期采样32点，前后两路相差62μs，采用32点FFT计算，本方法与16点均方根法计算结果相同，U=1.437，I=2.1307，P=2.6414，有相同的精度。不校正时的 P=2.6718，相对误差达1.151%，误差较大。
由数字信号处理的理论知道，用DFT进行频谱分析时会产生混叠现象、栅栏效应和截断效应，因此，会产生误差。混叠现象可以通过在采样前进行模拟滤波消除，因消除的谐波次数较高，对测量的影响很小。由于电量中只含有有限次的谐波分量，其频谱可以从N个缝隙中看到，栅栏效应的影响基本没有。另外，电量中各次谐波的谱线是离散的，采样截断后频谱中的谱线向附近展宽影响较小，谱间干扰也较小，因此，截断效应的影响很小。DFT隐含周期性，当频率变化时会产生误差，这可以通过自适应调整采样时间间隔来消除。综上所述，由于电力系统正常运行时，畸变电量中一般只含有基波和其整倍数次高次谐波，因此，采用软件的方法，用顺序采样值，可以实现畸变电量的精确测量。
4结论
利用顺序采样值，用软件的方法得到同一时刻各电压、电流的基波和各高次谐波向量，可以实现畸变电量的精确测量，对降低测量保护装置硬件成本，提高测量保护装置的可靠性和测量精度有重要意义，具有实用价值。
参考文献
［1］孙淑信. 变电站微机检测与控制［M］. 水利电力出版社，1995.5.
［2］黄益庄. 变电站综合自动化技术［M］. 中国电力出版社，2000.3.
［3］毕胜春. 电力系统远动及调度自动化［M］. 中国电力出版社，2000.4.
［4］于海生,等. 基于复序列FFT和锁相原理的电参数测量［Ｊ］.电网技术，2000.24(3).
［5］邱关源. 电路（第三版）［M］. 高等教育出版社，1989.
网友评论：（只显示最新10条。评论内容只代表网友观点，与本站立场无关！）
