张兴福
北京理工大学化工与材料学院,100081
0 引 言
由于实际中的工业过程通常具有未知、时变和非线性等特性,所以使用固定参数的控制器,在满足控制要求方面会受到许多限制。而在这种情况下,自适应控制策略就显得优越得多了。因此,根据自适应控制的思想,研究如何提高控制系统的稳定性,消除控制系统的残差,是具有重要的理论意义和应用价值的。
普遍认为,过程工业中存在的时滞问题,特别是变时滞和随机扰动问题,是影响控制系统的稳定性和控制品质的重要因素。多年来,变时滞和随机扰动过程的控制问题一直吸引着众多的研究者,并先后提出了许多解决方法。在众多的控制算法中,Kurz提出的扩展B多项式法[1]、Wellstead的方法[2]和Clarke提出的方法[3],能够成功地应用于变时滞过程。但系统中扰动快时变或是随机阶跃扰动的时候[4][5],它就不能很好地满足控制要求了。
本文介绍的这种算法是基于CARIMAControllenAuto-RegressiveIntegeratedMoving-Average)模型,用该模型描述实际的受控过程,比常用的CARMA模型要好[6][7]。对变时滞和未知扰动过程,通过1步向前预报辅助函数的方法,提出一种自校正算法,采用递推估算法来辩识参数,使设计的控制器性能得以改善。最后,针对一个受控过程的数学模型进行了仿真研究,试验结果显示了这种控制算法良好的控制性能。
1 模型描述及控制规律
用下面的模型表述一个工业过程:
Ay(t)=q-kpBu(t)+ξ(t)/△ (1)
这里y(t)、u(t)和ξ(t)分别代表系统的输出、输入和干扰项;ξ(t)是均值为零方差σ2的不相关随机扰动;A、B是q-1的多项式;△=1-q-1后移位算子;kp是受控过程的时滞。
为了获得更实用的控制算法,能够处理广泛存在的非最小相位问题,这里只研究保留全部过程零
点的情况。
1.1 控制算法
定义辅助函数
ø(t+1)=Py(t+1)+Q△u-Rw(t) (2)
其中加权项P、Q和R是q-1的多项式;1是向前预报的值。
利用恒等多项式
P/A=L△+q-1G/A (3)
其中L和G是q-1的多项式。
将(3)式代入(1)式得

则控制规律可取为
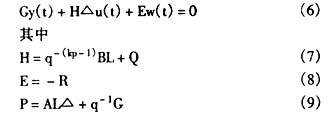
将式(1)两边同乘以H,利用式(6)并简化得

在特征多项式中,出现了q-(kp-1)项,这正是由于控制算法不是kp步向前预报,而是1步向前预报的结果。
1.2 加权项的选择
对于保留全部过程零点的情况

其中T(q-1)是希望的闭环系统的特征多项式。
根据式(12)来调整P、Q,可以保证系统的特征多项式与希望的特征多项式相同。使系统始终保持其稳定性;根据式(13)来选择R,可以实现系统输出对给定值的静态无差跟踪。
1.3 控制算法的实现
为了避免P、Q和R在线调整与参数估计间的相互影响,这里通过定义P具有下列结构来实现

这里令

这时P、Q和R按照式(12)和式(13)进行在线调整时,就不会对参数估计的结果产生影响。
根据式(14)和(15),方程式(12)可写为

式中,α为引入标量,且α=b0+Q0
方程式(13)亦可重新表示为

2 控制算法流程

(3)控制多项式的综合

(4)控制规律
H△u+Gy(t)+Ew(t)=0
(5)每个采样周期重复上述各步。
3 仿真研究
我们选择仿真对象的模型为

其中,kp:受控对象的时滞(1≤kp≤3);
δ(t):随机阶跃扰动(0≤δ(t)≤1);
ξ(t):方差为0.01的白噪声。
由于CARIMA模型使用增量型的数据向量,所以能够自动产生积分作用,保证系统有随机阶跃扰动时,无稳态输出误差。从图1充分说明了这一点。(前60个采样周期采用PID控制)。
在t=210时,δ(t)突然从0变到1,这一变化立刻影响到系统的输出。由于CARIMA模型产生的积分作用,很快地消除了它的影响,使系统继续保持原有的控制效果。

在t=240时,kp突然从3降到1,此时辩识算法中的遗忘因子迅速减少,依靠辩识结果,加权项P和Q不断地得到调整,使系统在时滞变化的情况下,仍能稳定运行。
在t=330时,δ(t)突然从1变到0,但它的影响马上又被克服了。
4 结 论
通过仿真研究可以发现,基于CARIMA模型1步向前预报的自适应控制算法,不仅可以解决变时滞问题,而且还能快速消除未知扰动的影响。所以对工业过程具有良好的控制效果。
参考文献
1 Kurz H.Digital parameter adaptiver control of process with un-known constantortime varying dead time[Z].5th IFAC Symp On Ident and Syst Para Esti Germany,1979
2 Wellstead PEDPrager and PIanker.Pole Assignmentself-tun-ingregulator[J] .Proc.IEE.1979,126:781~787
3 Clarke DW.Implementation of self-tuning controllers self-tuning and adaptive control[J].Theory and Applications,1981,ch6
4 De Keyser RMCand Van Cauwenberghe AR.Self-tuning loadfollowing controlofa nuclearpower plant[Z].IFACSyposiumonAutomated Control in Power Generation and Distribution and Protection Pretoria,1981
5 Friedand Band SM Grabousky.Estimating sudden changes ofbi-asesin linear dynamic systems[J].IEEETrans 1952,AC-27:237~240
6 Tuffs PSand Clarke Dw.Self-tuning controlofoffset[J].AU-nified Approa ch. Proc .IEE.1985,132:100~110
7 Scattolini R.Amultivariable self-tuning controller withintegralaction[J].Automatica,1986,22:619~627
8 徐宏跃,胡锡恒.时变后系统的鲁棒性保护-时滞跟踪自适应控制[C].贵州工学院科学论文集,1981
|


