高 山 单渊达
东南大学电气工程系 210096 南京
0 引言
在电力系统计划与运行管理中,负荷预测决定了发电、输电和电能分配等方面的合理安排问题,对电力系统的安全、经济运行与国民经济的发展具有非常重要的影响。其中,未来24 h负荷预测是电力系统调度管理部门制订开停机计划及在线安全分析的基础,也是电力市场中实现电能计划管理的基础。
1991年D.C.Park等人首次将人工神经网络(ANN)方法引入负荷预测[1,2],引起了研究人员的广泛兴趣。现有的ANN方法一般采用BP算法的前传多层感知器网络,由于感知器网络权重初始化的随机性,难以根据负荷预测的实际情况确定一组较好的初始值,并且BP算法学习收敛速度较慢,容易陷于局部极小点,从而极大地限制了神经网络方法在负荷预测中的实际应用。近年来发展起来的径向基函数(radial basis function, 简称RBF)理论为前传网络的学习提供了一种新颖而有效的手段[3]。RBF网络具有良好的推广能力,而且学习比通常的BP方法快得多,具有广阔的应用前景。
本文从短期负荷预测的实际应用出发,将径向基函数网络引入负荷预测,综合考虑了不同类型日(工作日、休息日、节日)、最高温度、最低温度、气候(阴、晴、雨、雪)等因素对负荷的影响。基于本文方法完成的软件包已在国内若干供电局投入现场运行。
1 RBF网络及其算法
1.1 RBF网络简介
RBF网络[3]通常是一种两层前传网络,某一维输出的RBF网络的输入输出关系可以利用一组归一化的径向基函数构造的映射fr来表示:
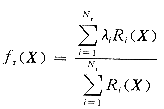
(1)
其中 Nr为隐层节点数;Ri(X)为隐层节点的基函数;λi为网络的输出层节点同隐层节点的连接权。
Ri(X)对输入激励X产生一个局部的响应,即仅当输入落在输入空间中一个很小的指定区域中时,隐单元才作出有意义的非零响应,输出层节点实现隐层节点非线性基函数输出的线性组合。
从理论上说,和一般多层感知器(MLP)网络一样,RBF网络能以任意精度逼近任意非线性映射。
本文中隐层节点的基函数采用了一种“高斯条”(gassian bar)函数,它是将每个输入维的高斯响应加权求和:

(2)
其中 i表示第i个高斯条单元(即隐层节点i);j表示输入维;M为其维数;xj和cij,σij,wij分别是输入向量X和第i个高斯条函数的中心Ci、宽度σi以及权矢量Wi的第j项。
1.2 RBF网络参数的初始化
RBF网络应用的关键是隐层节点基函数中心的选取。在实践中,可以采用适当方法将中心取为样本数据的某个子集。中心确定以后,可以根据中心同样本数据的某种测度关系得到相应的宽度。这样RBF网络中隐层基函数的中心和宽度在网络初始化时就可基本确定,在网络学习中只需作很小的修正,比起所有初始参数都是随机确定的多层感知器网络来说,RBF网络的学习收敛速度当然快得多。并且隐层基函数中心的选取,可以根据要解决问题的不同而采用不同的策略,选取最有利于问题解决的基函数中心。
对采用式(2)高斯条函数的隐层节点初始化时需要确定3种参数:第i个隐单元基函数的中心Ci、宽度σi以及权矢量Wi。首先,利用N(N-1>Nr)个样本输入矢量X来计算Nr个Ci,目的是使Ci尽可能均匀地对输入数据抽样,使Ci能够反映输入矢量在输入空间中的分布情况,在输入矢量集中的地方选中的Ci也多,因此对隐层节点基函数中心的初始化过程就是对样本输入特性认识和分类的过程。对Ci初始化可采用k—均值聚类算法,将样本输入数据分为Nr类,每一类的聚类中心就作为相应隐单元基函数的中心。k—均值聚类算法不仅简单,而且性能良好,在模式识别中应用十分广泛。其具体过程在各种模式识别书籍中都有详细的介绍[4],这里就不再赘述。基函数中心Ci找到以后,就可以求得其宽度σi,它们表示与每个中心相联系的数据散布的一种测度。可令它们等于聚类中心与训练样本之间的平均距离,即
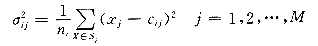
(3)
其中 Si是所有属于第i类的样本输入X的集合;ni为Si中样本的个数。
权矢量Wi的每一分量wij初始化时可取1。输出层节点同隐层节点的连接权λi初始化时可取一较小的随机数。
RBF网络中的大部分参数可以根据实际问题在初始化时给出较好的初始值,从而为快速训练奠定了基础。
1.3 RBF网络的快速混合学习算法
当各种参数初始化完成以后,RBF网络作为前传神经网络的一种,同样可以采用BP方法进行网络训练和学习。即利用一组输入矢量{Xk,k=1,2,…,N}及其映射{yk,k=1,2,…,N}组成的样本,采用梯度算法使价值函数E最小,以达到调节权的目的,
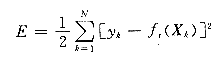
(4)
但BP算法固有的缺点限制了RBF网络优点的体现。根据RBF网络的特点,本文采用了一种结合梯度方法和最小二乘方法的快速混合算法,有效地解决了RBF网络的学习问题。
假设现有一单输出的RBF网络,其隐层节点个数为Nr。设有N个样本,(Xk,yk)(k=1,2,…,N),并设RBF网络各隐层节点函数的中心和宽度已经初始化。由于RBF网络的输出层对隐单元的输出进行线性加权组合,因此对于输出层节点和隐层节点的连接权这一部分参数可以得到一个形如式(5)的矩阵方程:
AZ=B
(5)
其中 A是N×Nr维的矩阵,其行向量aTk相应于样本输入Xk的隐层节点输出;B是N×1维的矩阵,其第k个元素bk相应于样本输入Xk的网络期望输出yk;Z是Nr×1维矩阵,相应于隐层节点同输出层的连接权,即待求矩阵。
由于一般样本数目N远大于待求参数数目Nr,即方程的个数多于未知数的个数,因此只能以估计理论的处理方法来解方程。
本文采用了一种迭代公式来求取Z的估计值[5]:
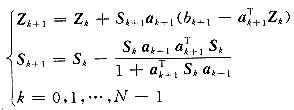
(6)
其中 aTk为矩阵A的第k个行向量;bk+1是矩阵B的第k+1个元素;Sk是Nr×Nr维的协方差矩阵;Z的最小二乘估计值就是ZN。
式(6)的初始状态是:
Z0=0, S0=γI
(7)
其中 γ是一个很大的正数,一般可取1000,I为Nr×Nr维的单位矩阵。
式(6)同样适用于多维输出的情况,可用bTk+1代替式(6)中的bk+1,bTk+1是矩阵B第k+1个行向量,它相应于样本输入Xk+1的多维网络期望输出值。
快速混合算法参数的修正过程可分为以下步骤。
a.前向过程:固定每个隐单元高斯函数的中心Ci、宽度σi和权矢量Wi不变,对每一个样本输入,计算隐单元的输出,形成矩阵A的相应行向量。遍历所有的样本,形成矩阵A,其相应的样本输出形成矩阵B。然后利用式(6),求出参数Z,即隐单元到输出层的连接权。
b.后向过程:固定前向过程中求出的隐单元到输出层的连接权不变,对每一个样本输入,求出其相应的网络实际输出,根据实际输出和期望输出的差值,用负梯度的方法,修正隐单元中的参数(高斯条函数的中心、宽度和权矢量)。
c.循环上述两过程,直到误差达到要求或循环次数达到一定值。
实践证明,快速混合算法十分有效。事实上,对于任一种网络,设其参数集S可分解为两部分:S=S1S2(为直积)。如果S2同网络输出线性相关,或S2经某种函数变换后同网络输出线性相关,就可以利用上述快速混合算法对网络进行学习。
快速混合惴ǜ軷BF网络的特点,对网络中初始化时随机确定的参数λi的修正找到了新的思路和方法。使网络参数在最初几步就到达最优点附近,从而避免了学习中不必要的振荡,减少了陷入局部极小点的可能性,保证了网络学习的可靠性和精度。
2 基于RBF网络的短期负荷预测
地区负荷同天气、季节、节假日等因素密切相关,如雨、雪等天气情况会明显改变负荷的大小与形状,同样高温和严寒天气也会改变负荷的幅值和曲线形状,元旦、春节等节日的负荷与平时也有明显不同。这样,诸多因素影响的复杂性使得地区级负荷波动频繁。因此,地区级负荷的预测问题一直是负荷预测中的难点问题。
神经网络预测方法中最重要的是样本的选择问题。其包括两方面:①选择样本输入与样本输出的关系;②选择合适的样本集。
一般工作日负荷有如下关系:某一天的负荷曲线同其前一天的负荷曲线比较相似,同其一星期前的同一天的负荷曲线也比较相似;一天中某一点的负荷同前几天同一点的负荷相差不大。即可认为一天中的某一点负荷与前一天同一点附近的负荷,与前几天同一点负荷,与一星期前同日同一点附近的负荷相关性比较大。为降低问题的求解规模,对一天24 h每一小时负荷的预测分别建立其单独的预测模型。因此针对一天中第i小时负荷可以建立如下的输入输出关系:
Li,t=f(Li-1,t-1,Li,t-1,Li+1,t-1,Li,t-2,
Li,t-3,Li-1,t-7,Li,t-7,Li+1,t-7)
(8)
式中 Li,t表示第t天第i小时的负荷。
式(8)仅针对工作日而言。在样本选择时要尽量选择与要预报日相同类型日的样本。当预报日前几天中包含节假日时,节假日负荷的存在会严重影响预测的精度,需要根据节假日日历日期,选择前若干天中与其天气情况相近的工作日或休息日负荷代替节假日负荷。由于节假日负荷同平时负荷相差很大,式(8)不再适用,要单独考虑其预测问题。
本文在样本集选择时主要考虑了4种环境因素的影响:r(日期类型),W(天气),ht(日最高温度),lt(日最低温度)。首先将每一天的环境因素数值化,例如对r分量用1表示工作日、2表示周末、3表示节日;对W分量可以用1表示晴天、2表示阴天、3表示下雨,或更细致地将天气因素区分为晴、多云、阴、小雨、中雨、大雨、小雪、中雪、大雪等;对ht和lt分量可用温度的实际值表示。确定了各环境因素后就可得到每一天的环境向量E,根据E中各分量对负荷影响程度的不同,采用相应的策略就可以得到需要的样本集。
现以一工作日的预测为例介绍样本集的选择方法。假设已知某一工作日的负荷环境向量E0(r0,w0,ht0,lt0),要预测的工作日的环境向量为E1(r1,w1,ht1,lt1)。在前一二年的负荷记录中选择与这两天有相似环境关系的负荷作为备选样本,假设一备选样本的环境向量分别为Ei0(ri0,wi0,hti0,lti0)和Ei1(ri1,wi1,hti1,lti1),计算该备选样本同预测目标的环境偏差d:
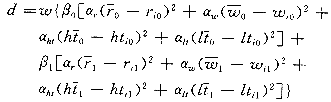
(9)
其中 w为按样本离预测日时间近大远小原则选择的权重;β0,β1表示前后两天的环境偏差在总的环境偏差中的不同影响;αr,αw,αht,αlt是表示各环境分量对负荷影响程度的权重。
αr要给一较大的权值,使不同类型日的预测可以区别开来,适当选择各权重就可以得到一个按环境偏差从小到大排列的备选样本集,从中选择出一定数目(如30个)较相近的样本作为网络的初始化样本,再在初始化样本中选出最相近的几个,一般6~8个,作为训练样本。
3 算例
某地区短期负荷预测结果实例见表1。
表1 某地区短期负荷预测结果实例
Table 1 Some short-term load forecasting results
in a certain region
日期
星期
平均误差/(%)
1998-05-04
星期一
3.5
1998-05-05
星期二
2.9
1998-05-06
星期三
2.3
1998-05-07
星期四
2.9
1998-05-08
星期五
2.5
1998-05-09
星期六
2.2
1998-05-10
星期日
3.3
从以上预测实例可以看出:基于RBF神经网络的短期负荷预测为地区负荷的预测问题提供了一种可行的方法。不同地区负荷的特性不同,影响负荷的因素也不完全相同,因此预测时对输入输出关系的选择和样本集的构成,要针对不同地区的特点作必要的调整。现在该程序已在若干供电局投入实际运行,其平均误差基本上在5%以内,我们正在根据现场的反馈来进一步分析数据和完善程序,使它更能满足实用化的要求。
|


