覃 剑 陈祥训 郑健超
国家电力公司电力科学研究院,100085 北京
1 前言
电力系统的发展对其经济性、安全性和可靠性提出了更高的要求。因此,利用故障产生的行波快速切除故障线路的行波保护,在输电线继电保护方面得到了广泛应用[1]。同时利用行波进行故障定位,能克服阻抗法易受对侧系统运行阻抗、负荷电流、系统运行方式等因素影响的缺点,使得测距精度得以提高[2~4]。
在实际输电线路中,由于线路结构变化,换位方式不同,输电线沿线大地电阻率的不均匀,线路参数随频率的变化,行波色散等问题,使得行波分析和研究比较困难,故障产生行波的特点不能被充分利用。因此对行波在输电线上传播时的色散规律,行波特征,输电线路参数及不同故障类型时行波传播特点等进行深入研究非常必要。本文主要讨论不同故障类型情况下行波的传播特点。
2 行波研究的线路模型
输电线路电磁暂态的数字仿真可在时域或频域中进行。在时域中的计算方法主要有网格法和特征线法两种。特征线法是以描述输电线路波过程规律的贝瑞隆(Bergeron)公式及其相应的等值电路为基础来进行网络的暂态仿真。其计算速度较快,在求解复杂电网和非线性元件方面,有较大的适应能力,适于研究暂态的全过程,因而得到广泛应用。在频域中的计算方法主要有改进的傅氏变换法。它是根据傅氏变换先在频域中求得电压、电流的频域响应,再用数值积分反变换到时域,得到时域解。其缺点是计算量大,而且由于采用傅氏变换而对非线性元件的适应能力较差。但它能精确地考虑大地电导率为有限值而导致的线路参数的频率相关性,这使它又优于其它方法。本文研究中所使用的电磁暂态程序(EMTP)就是使用了特征线法并辅以改进的傅氏变换法同时计及线路参数的依频变化。
由于线路参数的依频变化,尤其是线路单位长度的电阻和电感的频率相关性在零序模中最为突出,所以频率相关性的线路模型对单相接地故障这类含有显著的零序电压和电流的暂态类型是很重要的。研究由各种短路故障产生的含有较高频率分量的行波信号时,用多个T型和Π型等值输电线路模型就很难满足要求[5],线路较长时,更是如此,而且会产生由于参数集中而引起的虚假振荡,因此必须采用频率相关模型[6,7]。本文主要针对500 kV线路电压行波在输电线上传播的仿真研究,采用的是频率相关模型。它通过相-模转换矩阵由模量来对相量情况进行分析。分析的线路采用以B相为中间相,以A、C相为边相的中心对称的平行线路布置,四分裂导线,分段地线,不换位线路,大地电阻率取较为常见的计算耕土、黑土等所用的电阻率100 Ω*m[8],行波采样频率为1 MHz。线路上各点电压行波为该点发生短路故障后的电压减去未发生故障时该点正常运行电压。为方便比较,分析所用各点电压行波都从电压行波初次到达该点算起,这样做不影响对行波传播规律的分析,因为这只是将不同传播距离的行波在时间轴上作了平移而已。文中数据窗长度的选取原则是以能反映所考虑的模式的色散情况为准。
3 故障类型对行波传播的影响
输电线路发生短路故障时,测量点故障行波中各模频率分量受许多因素影响,如故障点的位置、线路参数和故障类型等。
3.1 单相短路故障
设A相金属接地短路(接地电阻为10 Ω),故障时A相电压相角为-92.7。短路故障产生电压行波在输电线上传播了120 km后,在三相上由模量组成的行波相量波形如图1(a)所示,图1(b)为其线模部分放大图。由图可见,B相只有地模(模1)和模3分量,不存在模2分量。其中地模分量幅值与A相的地模基本相同,且方向也相同;而模3分量的幅值约为A相模3分量的2倍,但方向相反。C相三个模的分量都存在,其中地模与A相、B相的地模分量幅值基本相同,方向相同;模2分量与A相模2分量幅值基本相等,方向相反;模3分量与A相的模3分量幅值相等,方向相同。这样可以推出模1(地模)、模2和模3在各相上的传播规律,如图2所示,图3为各相上各模的传播规律。

(a)色散引起的行波传播失真图
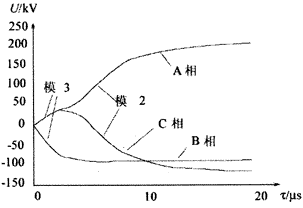
(b)线模部分放大图
图1 行波在三相上传播色散图
Fig.1 Dispertion waveform of travelling wave
propagation in three-phase

图2 各模在各相上传播
Fig.2 Each mode propagation in each phase
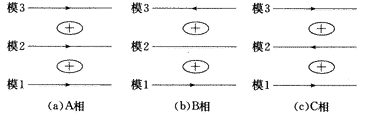
图3 各相上各模的传播
Fig.3 Each mode propagation in each phase
因此对三相水平排列的线路,各个模分量之间的关系为:
对地模分量有: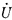 A(1)= A(1)=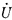 C(1), C(1),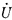 B(1)=m B(1)=m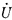 A(1),m≈1 A(1),m≈1
对模2分量有: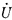 A(2)=- A(2)=-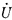 C(2), C(2),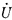 B(2)=0 B(2)=0
对模3分量有: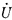 A(3)= A(3)=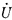 C(3), C(3),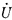 B(3)=n B(3)=n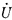 A(3),n≈-2 A(3),n≈-2
这里的m和n称为模系数。理想情况(三相完全对称且无架空地线)下的m=1,n=-2。对有地线的实际线路而言,模系数主要由线路参数和结构决定。
对于其它形式排列的三相线路(如三角排列),可以由EMTP程序或其它方法求出被分析线路的特征向量矩阵,由相-模转换关系可推出被分析线路的各模在各相上的传播图或各相上各模的传播图。本文不再详细分析。
明确了以上关系后,就可由任一相上行波波形中各模的幅值及方向推断出另两相行波的各模的大致幅值及方向,即可确定另两相上行波的波形。
由于行波在A相和B相上的传播模式不同,必然使行波在A相或B相传播时的衰减和相位延迟情况有所不同。下面讨论当B相故障时,行波在B相传播时的色散情况。
设B相金属接地短路(接地电阻为10 Ω),故障时B相电压相角为-92.7。图4(a)为B相短路行波传播120 km后由模量组成的三相行波相量波形图,图4(b)为其线模的部分放大图。由图可见,行波在B相传播时,地模约占行波幅值的50 %,线模约占50 %。对照图1(b)和图4(b)可知,线模中都是模3分量。行波在B相传播时,地模的色散情况与A相基本相同,不同的只是行波的上升沿斜率。行波前沿在B相以模3各频率分量的相速传播,它的衰减常数较小,因此行波中的高频分量比在A相中要高。
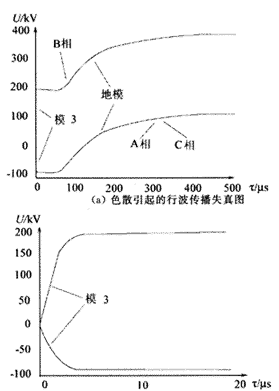
(b)线模部分放大图
图4 行波在三相上传播的色散图
Fig.4 Dispertion waveform of travelling wave propagation in three-phase
所以行波在B相中传播时,上升沿斜率较高。
单相短路故障时,非故障相行波是通过空间耦合过去的,只有故障相产生的行波模式才能在非故障相中出现。由于B相短路故障只有地模和模3分量,所以A、C相此时也只有与B相幅值基本相等、方向相同的地模分量,模3分量的幅值约为B相模3幅值的一半,方向相反。
A相和C相都是以B相为中心对称布置的边相,因此,C相接地短路故障完全与A相短路故障相同,本文不再重复。
由于故障相行波是各个模分量的叠加,且各个模分量同号,因此故障相行波幅值较大。而非故障相的行波虽也是由各个模分量叠加,但各模分量不会是同号,因而造成非故障相行波幅值较低。非故障相的地模与模2或模3符号相反,使非故障相中线模的作用突出,如图1中B相模3突出,C相模2突出。
以上规律可用作判断单相故障类型的依据。行波幅值最大的一相中,地模若约占行波幅值的50%,则可断定是单相故障,幅值最大的即为故障相。
3.2 两相金属短路和两相对地短路故障
设A相与B相通过10 Ω电阻短路,故障时A相电压相角为-92.7。A相和B相故障点对地行波及其传播120 km后的波形如图5(a)所示,图5(b)为其线模部分放大图(B相对地行波为负值,图中取负号)。由图可见,AB相短路所产生的行波中基本上都是线模,这是由于行波源是在A相与B相之间产生的。它与大地没有构成回路,因此行波在传播过程中的色散现象不明显。A相中行波模2和模3共同起作用,B相中行波模3起主要作用,因而导致行波在A相和B相中传播时的上升沿斜率不同,B相大,A相小。这与A相或B相单相对地短路的情况基本相同。由于地模影响可不考虑,故障点在A、B相产生的行波幅值基本相同,而且在A、B相上的行波传播一段距离后,幅值仍会比较接近。
设A、B相接地短路(A、B相分别通过20 Ω电阻接地),故障时A相电压相角为-92.7。A相和B相故障点对地行波及其传播120 km后的波形如图5(c)所示,图5(d)为其线模部分放大图(B相对地行波取负号)。由图可见,AB相对地短路所产生的行波中,A相中地模约占1/4,线模约占3/4。其中模2占主要部分。B相中地模与模3方向相反,行波波前由模3起主要作用。A、B相行波之间相互影响较强,这从图5(d)中B相行波传播120 km后的行波幅值比故障点处的B相行波幅值还高可以看出。故障点处电压行波幅值由故障时故障相的电压相角决定,而行波传播过程中的幅值就与另一故障相行波幅值的大小密切相关。由于是相间对地短路,因此地模的影响比仅相间短路要大一些。
是相间短路还是相间对地短路故障,可通过行波幅值和行波中是否有地模分量作出判断。
3.3 三相金属短路和三相对地短路故障
设A、B、C相之间分别通过10 Ω电阻短路,故障时A相电压相角为-92.7。三相故障点对地行波及其传播120 km后的波形如图6(a)所示,图6(b)为其线模部分放大图(B、C相对地行波基本为负值,图中取负号)。由图可见,三相金属短路的行波中完全是线模分量,A相和C相行波中主要为模2,B相行波为模3,它们在传播过程中的色散很不明显。
设A、B、C相接地短路(三相分别通过30 Ω电阻接地),故障时A相电压相角为-92.7。三相故障点对地行波及其传播120 km后的波形如图6(c)所示,图6(d)为其线模部分放大图(B、C相对地行波基本为负值,图中取负号)。由图可见,三相对地短路的行波主要由线模决定,地模影响基本可不考虑。A、C相的行波中主要为模2,而B相行波中基本都是模3分量。三相金属接地短路的行波波形与三相金属短路的比较接近。
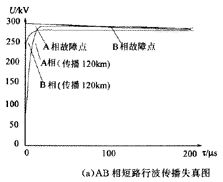
(a)AB相短路行波传播失真图
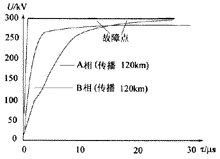
(b)线模部分放大图
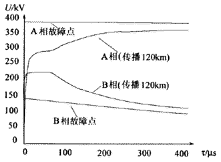
(c)AB相接地短路行波传播失真图
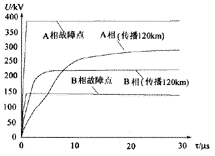
(d)线模部分放大图
图5 AB相间短路及AB相接地短路行波图
Fig.5 Dispertion waveform of travelling wave propagation of two-phase short-circuit and two-phase to earth short-circuit
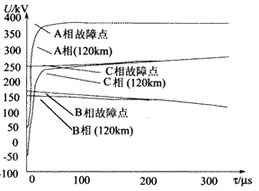
(a)三相相间短路行波传播失真图
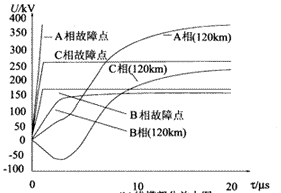
(b)线模部分放大图
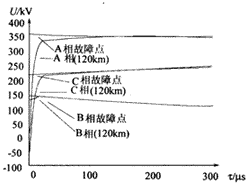
(c)三相接地短路行波传播失真图

(d)线模部分放大图
图6 三相相间短路和三相接地短路行波图
Fig.6 Dispertion waveform of travelling wave propagation of three-phase short-circuit and three-phase to earth short-circuit
4 小结
从故障的类型来看,单相故障所占比例最大,两相接地故障次之,两相、三相短路故障最少[9]。而行波中地模分量主要存在于单相接地短路时,两相接地短路中地模分量较弱,两相或三相短路中地模影响更小。所以在分析故障行波时,由于单相故障的概率最大,分析行波传播过程中的色散现象也显得非常重要了。但对两相相间或三相短路故障,地模的影响都可不考虑。这与分析故障稳态分量时,只有单相接地短路和两相接地短路时才有零序电压的结论是基本相同的。
故障行波在三相上以不同的模式传播,通过研究各种故障类型的行波及其色散特点,可以通过行波波形来判断故障类型;或当行波传播过程中色散较大,即地模和模2、模3之间可相互区分时(如行波传播较远),则可由任一相上行波的各模分量的幅值和方向,推断出另两相上行波的大致波形,并简单判断出故障类型。这样,就可采取合适的方法,利用由行波特征点确定的行波到达时间,进行故障测距,为精确故障测距打下了基础。
|


