胡登宇1陈彩屏2
1.长沙电力学院电力系,湖南省长沙市410077;2.湖南大学电气系,湖南省长沙市410082
1 引言
接地涉及电力系统的安全运行,是电力部门极为关注的问题之一。接地电阻的计算向来受电力部门所关注。由于土壤的电阻率并非常数,对竖直方向不均匀的土壤,常用二层土壤模型代替,再进行分析[5]。用建筑物基础中的钢筋作为接地体,具有耐腐蚀、可节约钢材和节省占地面积等优点,均匀土壤中水平或竖直对称地网基础接地电阻的计算可见文献[1]~[4]。建筑物的地基常是多层水平埋设与竖直埋设的钢筋复合体,其接地电阻无法用解析法计算。本文对二层土壤中这种复合地网的基础接地电阻,用矩量法与静电比拟法推导出计算式,并编制了相应的计算程序。
2 计算原理
设地中有一尺寸为a×b×H的矩形混凝土立方体(图1),内有一复合钢筋网,其水平网有K层,形状相同,外尺寸为L1×L2。第一层距地面为Z0,相邻两层距离为OZ,钢筋半径为r,竖直钢筋长为l,水平与竖直钢筋的半径可相等或不等,混凝土及二层土壤的电阻率分别为ρc、ρ1和ρ2,上层土壤厚度为HUP,设HUP>H。
由于是计算工频接地电阻,电流频率低,可按恒定电流场考虑。为了消去空气的影响 ,利用恒定电流场的镜象法将地面以下的部分对称地补充到地面以上来(如图2),它以地表面为对称面上下对称。用图2计算时,原钢筋和镜象钢筋必须流有相同的电流,以保证边界条件与图1相同,即地表面与电流线重合。根据唯一性定理,图1、图2下半空间场的解答相同 ,可用图2计算图1的电流场。根据静电比拟原理,将图2的恒定电流场转化为图2的静电场处理,为了保证εc/γc=ε1/γ1=ε2/γ2(其中γc、γ1和γ2为混凝土及土壤的导电系数),γc=1/ρc,γ1=1/ρ1,γ2=1/ρ2,故图2中的εc、ε1和ε2应分别取εc=1/ρc,ε1=1/ρ1,ε2=1/ρ2,这样,当给定电极电位φ0时,若能算出导体上的自由电荷Q,则可得出系统的对地电容C,由静电比拟法,可得出图2系统以及图1系统的接地电阻。

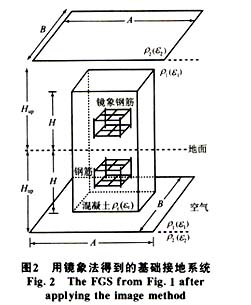
图2中,存在3种电介质εc、ε1和ε2,εc与ε1的分界面为六面立方体,ε1与ε2的分界面为无穷大平面,εc电介质内有导体,难以用解析法计算,宜用数值计算法求解。电介质在电场作用下被极化,在介质分界面上出现束缚电荷。为了便于后面用矩量法计算,设想将介质去掉,在介质εc、ε1的分界面上和介质ε1、ε2的分界面上放置束缚电荷,在介质εc内的接地电极上放置等效电荷,此等效电荷由束缚电荷及电极上的自由电荷所组成。当以束缚电荷代替电介质作用后,便可将图2的静电场看成置于真空ε0中,场域内任一点M(x,y,z)的电位可表示为
 (1) (1)
式中 s=s1+s2,s1为导体表面积,对应的σ为导体表面的等效面电荷密度,s2为介质分界面,对应的σ为介质分界面上的束缚电荷面密度;ds为面s上的面积元;rMP为源点P至场点M的距离。
设导体电位为φ0,当将场点M取在导体上时,导体钢筋上的电位为

在介质εc与ε1的分界面上,应满足边界条件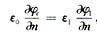 ,式中n为法线。用电荷密度σ来表示此式,利用式(1)分别算出此式中左右二项,在分界面P0点上,经推导可得[1,2] ,式中n为法线。用电荷密度σ来表示此式,利用式(1)分别算出此式中左右二项,在分界面P0点上,经推导可得[1,2]
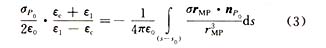
式中 s0为边界面上以点P0为球心、半径为无穷小的半球面;nP0为边界面上点P0处的法线矢量;σP0为P0处的束缚电荷面密度。

式(2)(3)(4)为积分方程,积分号内电荷密度σ(x,y,z)为待求量,用矩量法对这3式进行离散化,并求其数值解。以式(3)为例,水平网有K层,将每层剖分为m0个单元,水平钢筋上剖分数为mH=Km0,将竖直钢筋剖分为mV个单元。钢筋上总的剖分数为m=mH+mV。将介质εc与ε1的分界面剖分为m1个单元,介质ε1与ε2的分界面为无穷大平面,取有限大面积A×B近似代替(图2),将其剖分为N-m-m1个单元,N是系统总剖分数。选脉冲函数为基函数,意味着每个剖分单元面积sj上的面电荷密度σj为常数,则电荷密度σ可表示为σ=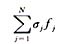 ,其中fj取1或0,当点(x,y,z)在sj内时,则取1,否则为0。再选狄拉克函数δ为权函数Wi,第i个剖分单元坐标定义为其面积中心,设点M的坐标为(x,y,z),点i的坐标为(xi,yi,zi),则有 ,其中fj取1或0,当点(x,y,z)在sj内时,则取1,否则为0。再选狄拉克函数δ为权函数Wi,第i个剖分单元坐标定义为其面积中心,设点M的坐标为(x,y,z),点i的坐标为(xi,yi,zi),则有

对式(3)应用矩量法,注意到P0是在分界面上的任意一点,且设其在分界面上的第i个单元上,则式(3)左边为
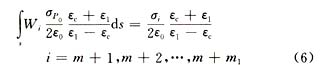
由于P0在第i个单元上,ds上的电荷面密度为σ,点P在ds上,则式(3)右边为
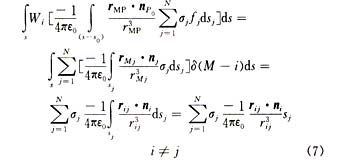
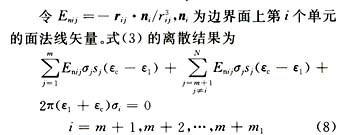
因系统上下对称,对称点上电荷密度相等,未知量仅为上半空间的电荷密度,只需对上半空间进行剖分,这样便可使方程数减少一半,节省了的内存,加快了运算速度。用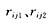 0分别表示源点j以及j在下半空间的对称点至场点i的距离。考虑到复合地网,则式(8)变为 0分别表示源点j以及j在下半空间的对称点至场点i的距离。考虑到复合地网,则式(8)变为
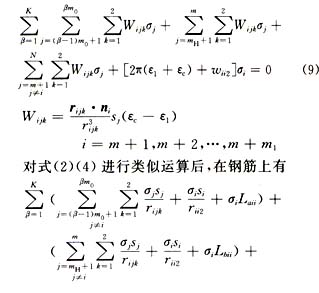
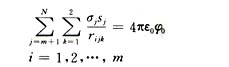
式中 第一项对应水平钢筋,第二项对应竖直钢筋,
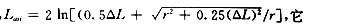
表示当i=j时,水平钢筋网上第i个剖分单元对其本身的电位系数,当i≠j时,Laii=0;Lbii的形式与Laii相同,它表示当i=j时,竖直钢筋上第i个剖分单元对其本身的电位系数 ,此时r表示竖直钢筋半径,当i≠j时,Lbii=0;σj为第j个剖分单元上的面电荷密度;sj为第j个剖分单元面积;ΔL为钢筋剖分单元长度;φ0为钢筋电位;N为系统剖分单元总数。
在介质ε1与ε2之分界面上有

式(9)(10)和(11)分别是式(3)(2)和(4)用矩量法离散后得出的线性代数方程,共N个。据此可进行编程,给定φ0后,用LU分解法解方程组,求出各单元上的电荷,算出钢筋上的总等效电荷Qeq= ,钢筋上的总自由电荷Q=(εc/ε0)Qeq,钢筋对地电容C=Q/φ0,前面已取εc=1/ρc,ε1=1/ρ1,ε2=1/ρ2,如计算时再设置ε0=1,φ0=1,则接地电阻R=1/C。 ,钢筋上的总自由电荷Q=(εc/ε0)Qeq,钢筋对地电容C=Q/φ0,前面已取εc=1/ρc,ε1=1/ρ1,ε2=1/ρ2,如计算时再设置ε0=1,φ0=1,则接地电阻R=1/C。
3 程序验证
均匀土壤和二层土壤接地电阻的计算以及均匀土壤基础接地电阻的计算均可看为本文方法的特例。以下用文献[7][8][9][4][3]的计算结果与本文程序计算结果进行比较。
(1)复合地网验证
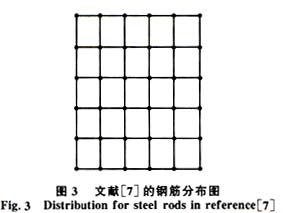
文献[7]对均匀土壤中一复合地网进行了计算,水平钢筋半径r=0.007 m,L1×L2=45.72 m×45.72 m,N1=N2=6,Z0=0.457 m,在每个节点上放置长为15.24 m、半径为0.007 94 m的竖直钢筋,共36根(图3),土壤电阻率为100Ωm,得接地电阻为0.774Ω 。文献[8]算得接地电阻为0.746Ω。本文程序中取ρ1=ρ2=ρc=100Ωm,算得接地电阻为0.755 3Ω。若将地网放入尺寸为a×b×H=50 m×50 m×18 m的混凝土中央,设土壤为二层,HUP=20 m,本文程序可算得:当ρc=99Ωm,ρ1=100Ωm,ρ2=101Ωm时,接地电阻为0.756 7Ω;当ρc=101Ωm,ρ1=100Ωm,ρ2=99Ωm时,接地电阻为0.754 0Ω。
(2)双层土壤验证
文献[9]给出双层土壤中方形水平地网接地电阻计算公式为

HUP<0.2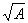 0;h<HUP;Cf为网格形状系数(正方形网格为0.9);ΔLx和ΔLy分别为网格在a与b方向的长度,m;L为网格导体总长,m;d0为导体直径,m;h为埋深,m;A0为地网总面积L1×L2,m2;HUP为上层土壤厚度,m;ρ1和ρ2分别为上、下层土壤的电阻率,Ωm。 0;h<HUP;Cf为网格形状系数(正方形网格为0.9);ΔLx和ΔLy分别为网格在a与b方向的长度,m;L为网格导体总长,m;d0为导体直径,m;h为埋深,m;A0为地网总面积L1×L2,m2;HUP为上层土壤厚度,m;ρ1和ρ2分别为上、下层土壤的电阻率,Ωm。
取h=Z0=2 m,ρ1 [1] [2] 下一页
|


