作者:张承慧,李洪斌
摘要:
0 引言
风机是一种量大面广、耗电量极大的动力机械。我国每年风机的电能消耗占总消耗的10%以上,在电力、钢铁、煤炭、冶炼工业中,风机的耗电量往往占生产用电的20%以上。因此,对风机的节能研究具有十分重要的经济意义。
风机系统中流量的调节常采用改变挡板开度的方式,因而在挡板上产生了附加的压力损失,浪费了大量能源。例如,热电厂中为锅炉燃烧提供空气的送风机,排除锅炉燃烧产生的高温烟气的吸风机,由于机组负荷经常变化,为了保证锅炉炉膛负压、烟气氧量及相应的汽温、汽压的稳定,需要及时调整送、吸风量及煤粉量。一般采用调整人口导向叶片的方式实现风量调节,叶片开度经常在60%~80%之间变化,这种叶片的节流损耗为风机额定容量的20%~ 30%[l,2]。采用变频调速技术改造风机系统,不仅可以节约能源,而且使系统运行更加合理可靠,这已成为广大工程技术人员的共识。但是,如何确定风机的调速比,使其运行在高效区,实现风机效率优化运行,尚鲜见文献报道。对于单台风机运行,问题较为简单;当多台风机并联或串联时,这实质上是一个非线性规划问题。
本文分析了风机系统的运行工况,根据管网特性分为两类系统,针对单台风机运行、多台并联、串联运行分析了最佳控制策略,确定最佳调速比[3] 。仿真实验表明该方法是有效的。新系统已在山东省某热电厂投入运行,取得了良好的经济、社会效益。
1 风机运行工况分析
1. 1 风机特性
风机的P-Q特性曲线(即压力—流量曲线)目前还不能用理论方法精确计算得出,而只能依靠实验方法[3] 。根据实验数据,风机在额定转速no下运行时,可按下述方程对其P—Q特性进行拟合:
P=Px-SxQ2 (1)
式中,Px和Sx为拟合参数。
应当指出,对于具有驼峰的P-Q特性曲线不符合上述方程。这种特性有可能使风机处于不稳定运行状态,并联运行时有可能出现喘振[1] ,选择风机时应避免,故本文不考虑该特性。
由风机的相似定理,当转速下调时,P-Q曲线平行下移[4] 。若转速下调到n1,则P—Q特性变为:
P=kPx—SxQ2 (2)
式中:k=(n1/no)2,为调速比。
根据η-Q特性曲线,Q过高或过低时,其效率η将急剧下降,故应限制流量范围为[Qmin,Qmaxl转速过低时,η也很低,故还应限制调速范围为[kmin,1]。这样可保证风机工作在高效区,如图1所示。
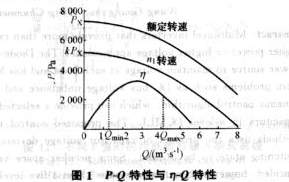
当多台风机并联工作时,通过将各风机在相同压力下的流量相加,可得并联后的P-Q特性;串联工作时,通过将各风机在相同流量下的压力相加,可得串联后的P-Q特性。两台风机并联和串联特性方程分别为:
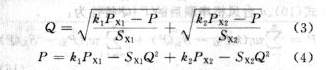
式中:ki,PXi,SXi为第i台风机的参数;i=1,2。
1.2 管网特性与系统分类
根据流体力学,当风流经管道时,受到阻力摩擦而产生的压力损失可由下式的管网特性表示:
R=PST+SQ2 (5)
式中:R为管网阻力;S为管网阻力系数;PST为系统的工作压力要求,即管网出口处压力高出风机引风口的压力值。
系统稳定运行时,风机实际提供的压力与R平衡,P—Q曲线与管网特性曲线的交点为风机的稳定工作点。
风机系统根据PST可大致分为两类:第1类系统的PST=0,即对工作压力无特殊要求,风机需根据负荷提供系统所需的流量,例如锅炉引风和送风系统、加热炉的助燃风机、矿井的通风系统等;第2类系统中流量无法由风机直接控制,主要由连接到管网上的用户端的阀门决定,风机需保证管网最不利用户端压力恒定,例如煤气输配系统。
1.3 节能原理
对于第1类系统,常采用调节挡板开度的方式来调节流量,这种方式实质上利用改变管网特性来改变风机工作点,如图2所示。
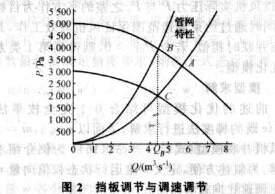
原风机工作在A点,若通过调节挡板使流量降低为QB,则风机将工作在B点,可见此时风机产生的压力不但没有减小,反而增大了,多余的能量浪费在挡板上。若调节风机转速,改变P-Q特性使工作点沿管网特性移动到C点,可恰好满足系统要求,使能量消耗大大减小。
对于第2类系统,常采用恒压调节方式。根据最不利条件下的流量QA和用户所需压力PST确定风机应提供的压力PA,选择风机参数使其工作在且点 (PA,QA)。
在运行过程中,只检测出风机出口处压力P,并根据P进行调度,使水压恒定在PA。若流量由QA减小到QB,风机工作点将沿水平线P=PA移动到C点(PA,QB)。但根据式(3),冈,机此时应提供的压力为PB:
PB=PST+SQB2 (6)
故多提供了PA-PB,这部分能量将消耗在管网中,浪费了能源。
若同时根据流量Q和用户所需压力PST进行调度,可解决上述问题。若流量由QA减小到QB,根据式(5)和检测到的流量QB,风机此时应提供的压力为PB。调度后风机将工作在最佳工作点B点(PB, QA),恰好满足用户需求。
可见,在这种调度过程中,风机工作点沿管网特性曲线移动,始终恰好满足用户需求且无能量浪费,节能效果最好,如图3所示。

所谓最节能的工作点,就是使风机的流量、压力恰好满足系统需要,使工作点沿管网特性移动,风机始终运行在P-Q曲线和原管网特性曲线的交点上。两类系统虽然要求不同,但是在调速策略上有很多相似之处。虽然第1类系统PST=0,但为了克服管网阻力R,风机仍要提供一定的压力P=R。因此,第1类系统可以看做是第2类系统PST=0时的特殊情况。下文对优化模型的分析仅限于第2类系统。
2 优化问题建模
2. 1 单台风机运行
假设某风机特性参数为PXi,SXi,ki,管网阻力系数为S。对于第2类系统,若压力要求为PST,Qe,为流量的期望值,则
R=PST+SQ2 (7)
k=[PST+(S+Sx)Qe2] / Px (8)
当PST=0时,可得第1类系统的调节方式。可见,单台风机运行问题比较简单,可直接获得调速比的解析表达式。
2.2 并联运行
假设某系统有n台风机并联运行,其中第i台风机为调速风机,i=1,2,……,m;m P=Pxi-SXiQ2 i=m=1,m=2,……,n (10)

此模型以各台风机实际流量之和∑Qi与Qe之差的平方作为目标函数,同时通过约束调速范围保证风机高效工作。式(13)、式(14)中的λi,ci,di表示风机高效工作时的调速范围和流量范围约束kmin,Qmin,Qmax,通过计算Qmin,Qmax。下的最佳工作点调速比并与λi,1比较,使高效工作的约束条件只用调速范围[αi,βi]来表示,简化了模型。ωi表示第i台风机的工作状态(1表示工作,0表示不工作)。在模型(式(11)~式(15))中,令PST=0,即得到第1类系统的优化模型。
2.3 串联运行
风机特性及管网参数同并联运行的式(9)和式(10)。n台风机串联后的P-Q特性为:
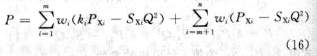
对于第2类系统,若系统要求工作压力为PST,Qe为流量的期望值,则应提供的压力Pe为 :
Pe=R=PST+SQe2 (17)
为使风机运行在最佳工作点,建立优化模型如下:

此模型的λi,ci,di,ωi参数与并联运行模型相同,以风机实际压力P与Pe之差的平方作为目标函数,同时通过约束调速范围保证风机高效工作,其思路与并联时相似。若令PST=0,则得到第1类系统的优化模型。
2.4 模型求解
前述的优化模型可结合0-1完全枚举法和 Wolfe既约梯度法进行求解。下面以n=5,m=2时多风机并联模型(式(11)~式(15))为例介绍求解步骤。为叙述方便,定义n维运行状态权值向量w和 m维调速比向量k:
w=[w1,w2,w3,w4,w5] (23)
k=[k1,k2] (24)
式中:w为各风机的运行状态向量;k为各调速风机的调速比向量。
模型求解步骤如下:
a.0-1完全枚举,这是从所有可行解中选出最优解的方法。当取w为某一确定值时,各台风机是否工作就完全确定,目标函数F仅随调速比七而变化。w的所有可能取值如表1所示,共31种,除去只开定速风机的7种组合,实际为24种。

然后再按照Wolfe既约梯度法进行求解。
c.比较各个w下的目标函数最优值,选取其中“最佳”者作为求解结果输出。此处最佳并不意味目标函数取值最小,因为在工程实际中,盲目追求精度是没有意义的。考虑到大型电机,尤其是定速风机的原动机,往往启动比较困难,故在摹本满足流量要求的条件下,启停动作越少越好。若存在多个w下的目标函数最优值满足精度要求,则按下式进行选择:
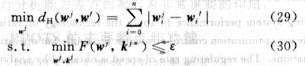
式中:wj为表1中w的各种可能取值;j为w取值的序号,j=1,2,……,31,且j≠4,8,12,16,20,24,28;i为向量w各分量的序号;ε为目标函数的精度要求;w'为当前运行状态的权值向量;kj*为wj时的最优点的调速比向量。
式(29)中按照Hamming距离来计算两向量之间的距离,其值等于两向量中对应元素不相等的个数,即启停次数。这样,可以保证以启停动作最少的最优解(w*,k*)作为求解结果。
3 仿真实验
使用数学软件MATLAB优化工具箱进行仿真计算,以n=5,m=2为例。风机参数为:调速风机PXl=30 kPa,PX2=20 kPa,SXl=48 Pa·m-3·s, SX2:20Pa·m-3·s,kmin=0.5;定速风机Px= 25 kPa,Sx=30 Pa·m-3·s。管网阻力系数S=100。
对于并联模型(式(11)~式(15)),若给定 (PST,Qe)=(10kPa,18.86 m3·s-1),则运行结果为:
w*=(1,0,1,0,0),k* =(0.582 1 ,0.80)
最优点的目标函数值为:
F* <10-4
由于定速风机容量相同,满足精度要求的解不止一组,例如:w18=(1,0,0,1,0),k18=(0.582 1, 0.80)等。此处应根据式(29)和式(30)选择启停次数最少的(w* ,k* )作为模型的解。可采用图解法对上述结果进行验证,即求P-Q特性曲线与管网特性曲线的交点,如图4和图5所示。可见,算法的精度是令人满意的。
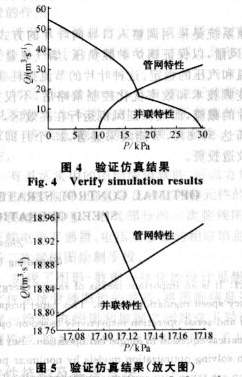
对于串联运行,可以采用与并联运行类似的方法,只需在求解算法和仿真程序中对目标函数做必要的修改,此处不再列出其详细步骤。假设风机的参数与并联运行时相同,若给定(PST,Qe)=(20kPa,6. 861 4m3·s-1),则运行结果为:
w*=(1,0,1,0,0),k*=(0.538 6,0.80)最优点的目标函数值为:
F*=5.449 8 X 10-10<10-4≈0
事实上,当w12=(0,1,l,0,0),k12=(0.80, 0.505 6)或w26=(1,1,0,1,0),k26=(0.538 6, o.80)等时,既约梯度法搜索到的目标函数值也能满足10-4精度要求,此时根据式(29)和式(30)来选择启停次数最少的解作为最优解。这里假设w*= (1,0,1,0,0)时,启停次数最少。
4 应用情况
目前,国内热电厂锅炉配备的送风机和引风机大多是单台运行或两台并联运行,单机容量很大。这种配置在定速传动时代是相对合理的,但在变频调速技术高度发展的今天就不再合 [1] [2] 下一页
|


