实际工程中有许多振动问题是非线性振动，例如油膜振荡、摩擦、旋转失速、流体动力激振等。线性振动系统与非线性振动系统的区分，往往取决于系统在激振力作用下的振幅大小。由于用线性振动理论能比较简便地研究和解决旋转机械系统的主要故障，所以在精度允许的情况下，可以把非线性振动问题线性化，作为线性振动来处理。但是在实际工程中，有些异常振动现象无法用线性振动理论来解释，而用非线性振动理论阐明故障机理，却很方便。非线性振动的主要特征如下。
(1)固有频率随振动幅值而变化
线性振动系统的固有频率只与系统的固有特性（k、m）有关，是一固定数值。而非线性振动系统则不同，其固有频率随振动系统的振幅大小而变化，如图1-12所示。
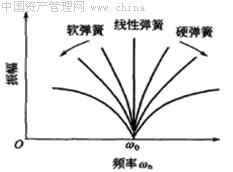
图1-12 自由振动的振幅与频率的关系
(2)振幅跳跃现象
具有非线性弹性的机械系统，在周期激振力作用下，振动可用强迫振动的基本成分ω与其高次谐波分量之和来表示。
据此可得到不同阻尼特性和振幅下的共振曲线，如图1-13所示。
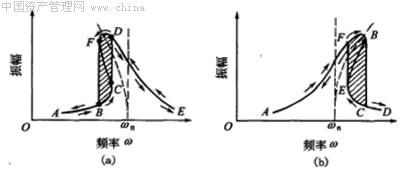
图1-13 共振曲线与跳跃现象
图（a)为软弹簧的情况，图(b)为硬弹簧的情况。在图(a)中，如将激励频率慢慢增大，振幅将沿曲线AB变化；在BC之间具有三个平衡点，而CF之间的平衡点是不稳定的平衡点。因此，从B移向C，一过C点就突然跳跃到D，然后进到E点，振幅发生突变。如将激励频率慢慢减少，从E下降的情况，经过的路程是从EDF跳跃到BA。在图（b)中，振幅也同样发生突变，这种现象称为振幅跳跃现象。
相位也有相同的跳跃现象。
(3)分数谐波共振和高频谐波共振
在非线性系统中，若以频率接近于固有频率整数倍的激励作用于系统发生共振时，以激励频率为基准，则共振的频率为激励频率的整数分之一，称为分数谐波共振。若激励频率接近于固有频率的整分数倍时，也会引起共振，这种共振称为高频谐波共振。
(4)组合共振（和差谐波共振）
在非线性系统中，若有两种不同频率ωl和ω2的激振力作用于系统，当它们的和（ωl＋ω2）、差（ω1-ω2）或（mω1士nω2）与固有频率一致时，往往也会引起共振，这种共振称为组合共振。
|
网友评论：（只显示最新10条。评论内容只代表网友观点，与本站立场无关！）
