|
随着机器转动速度的逐步提高,在大量生产实践中人们觉察到,当转子转速达到某一数值后,振动就大得使机组无法继续工作,似乎有一道不可逾越的速度屏障,即所谓临界转速。 Jeffcott用一个对称的单转子模型在理论上分析了这一现象,证明只要在振幅还未上升到危险程度时,迅速提高转速,越过临界转速点后,转子振幅会降下来。换句话说,转子在高速区存在着一个稳定的、振幅较小的、可以工作的区域。从此,旋转机械的设计、运行进入了一个新时期,效率高、重量轻的高速转子日益普遍。需要说明的是,从严格意义上讲,临界转速的值并不等于转子的固有频率,而且在临界转速时发生的剧烈振动与共振是不同的物理现象。
1.转子的临界转速
如果圆盘的质心G与转轴中心O′不重合,设e为圆盘的偏心距离,即O′G=e,如图1-2所示,当圆盘以角速度ω转动时,质心G的加速度在坐标上的位置为
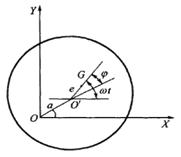
图1-2 圆盘质心位置
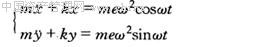 (1-5) (1-5)
参考式(1-2),则轴心O′的运动微分方程为
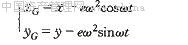 (1-6) (1-6)
令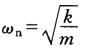 则: 则: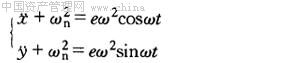 (1-7) (1-7)
式(1-7)中右边是不平衡质量所产生的激振力。令Z=x+iy,则式(1-7)的复变量形式为:
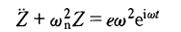 (1-8) (1-8)
其特解为 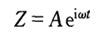 (1-9) (1-9)
代入式(1-8)后,可求得振幅
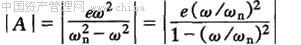 (1-10) (1-10)
由于不平衡质量造成圆盘或转轴振动响应的放大因子β为
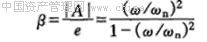 (1-11) (1-11)
由式(1-8)和式(1-11)可知,轴心O′的响应频率和偏心质量产生的激振力频率相同,而相位也相同(ω<ω。时)或相差180°(ω>ω。时)。这表明,圆盘转动时,图1-2的O、O′和G三点始终在同一直线上。这直线绕过O点而垂直于OX Y平面的轴以角速度。转动。O′点和G点作同步进动,两者的轨迹是半径不相等的同心圆,这是正常运转的情况。如果在某瞬时,转轴受一横向冲击,则圆盘中心O′同时有自然振动和强迫振动,其合成的运动是比较复杂的。O、O′和G三点不在同一直线上,而且涡动频率与转动角度不相等。实际上由于有外阻力作用,涡动是衰减的。经过一段时间,转子将恢复其正常的同步进动。
在正常运转的情况下,由式(1-10)可知:
(1)ω≤ωn时,A>0,O′点和G点在O点的同一侧,如图1-3(a)所示;
(2)ω>ωn 时,A<0,但A>e ,G在O和O′点之间,如图1-3(c)所示;
当ω≥ωn 时,A≈-e,或OO′≈-O′G,圆盘的质心G近似地落在固定点O,振动很小,转动反而比较平稳。这种情况称为“自动对心”。
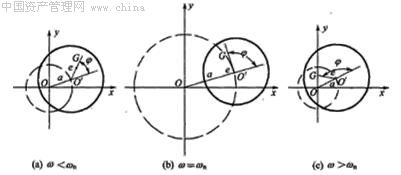
图1-3 转子质心的相位变化
(3)当ω=ωn时,A→∞,是共振情况。实际上由于存在阻尼,振幅A不是无穷大而是较大的有限值,转轴的振动非常剧烈,以致有可能断裂。ωn称为转轴的“临界角速度”;与其对应的每分钟的转数则称为“临界转速”,以nc表示,即
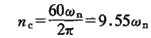
如果机器的工作转速小于临界转速,则称为刚性轴;如果工作转速高于临界转速,则称为柔性轴。由上面分析可知,具有柔性轴的旋转机器运转时较为平稳。但在启动过程中,要经过临界转速。如果缓慢启动,则经过临界转速时会发生剧烈的振动。
研究不平衡响应时如果考虑外阻尼力的作用(参见图1-14),则式(1-6)变为:
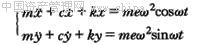 (1-12) (1-12)
令Z=x+iy,则上式的复变量形式为:
 (1-13) (1-13)
其特解为: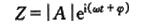
由此解得: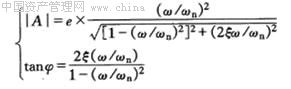 (1-14) (1-14)
式中 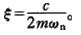
若令 
则式(1-14)可进一步写作: (1-15) (1-15)
这时的放大因子β为: 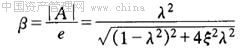
式(1-15)中振幅「A」与相位差φ随转动角速度与固有频率的比值λ=ω/ωn 改变的曲线,即幅值频响应曲线和相频响应曲线如图1-4所示。
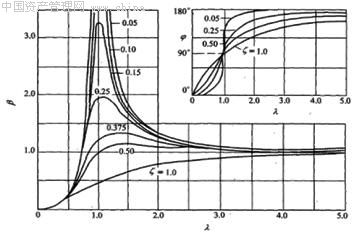
图1-4 幅频响应与相频响应曲线
从图1-4中可以看出,由于外阻尼的存在,转子中心O′对不平衡质量的响应在ω=ωn时不是无穷大而是有限值,而且不是最大值。最大值发生在ω>ωn的时候。对于实际的转子系统,把出现这最大值时的转速作为临界转速,在升速或降速过程中,用测量响应的办法来确定转子的临界转速,所得数据在升速时略大于前面所定义的临界转速n。,而在降速时则略小于nc。
2.影响临界转速的因素
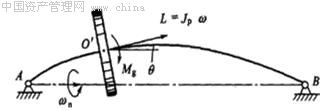
图1-5 转子系统中的陀螺力矩
(1)回转力矩对转子临界转速的影响
如图1-5所示,当转子上的圆盘不是安装在两支承的中点而是偏于一侧时,转轴变形后,圆盘的轴线与两支点A和B的连线有夹角θ。设圆盘的自转角速度为ω,转动惯量为Jp,则圆盘对质心O′的动量矩为 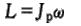 它与轴线AB的夹角也应该是θ,当转轴有自然振动时,设其频率为ωn。由于进动,圆盘的动量矩L将不断改变方向,因此有惯性力矩 它与轴线AB的夹角也应该是θ,当转轴有自然振动时,设其频率为ωn。由于进动,圆盘的动量矩L将不断改变方向,因此有惯性力矩
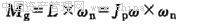 (1-16) (1-16)
方向与平面0′AB垂直,大小为 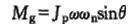 (1-17) (1-17)
因夹角θ较小,sinθ≈θ,故 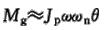 (1-18) (1-18)
这一惯性力矩称为回转力矩或陀螺力矩,它是圆盘加于转轴的力矩,与θ成正比,相当于弹性力矩。在正进动(0<θ<π/2)的情况下,它使转轴的变形减小,因而提高了转轴的弹性刚度,即提高了转子的临界角速度。在反进动(π/2<θ<π)的情况下,它使转轴的变形增大,从而降低了转轴的弹性刚度,即降低了转子的临界角速度。故陀螺力矩对转子临界转速的影响是:正进动时,它提高了临界转速;反进动时,它降低了临界转速。
(2)臂长附加力矩对转子刚度的影响
对较长的柔性转子,不平衡质量离心力作用点与转子和轴的连接点可能不重合而有一定臂长,与较短的转子相比,连接点处由同等离心力所产生的挠度将不一样,因为此时在计算连接点处的挠度时,要将力进行移位,而添加的等效力矩将改变轴的变形。分析表明,这种影响会使轴的挠度和转角增大,从而降低轴的临界转速(对柔性转子有利)。
(3)弹性支承对转子临界转速的影响
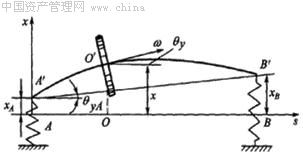
图1-6 弹性支承转子系统
只有在支承完全不变形的条件下,支点才会在转子运动时保持不动。实际上,支承不可能是绝对刚性不变形的,因而考虑支承的弹性变形时,支承就相当于弹簧与弹性转轴相串联,如图1-6所示。
支承与弹性转轴串联后,其总的弹性刚度要低于转轴本身的弹性刚度。因此,弹性支承可使转子的进动角速度或临界转速降低。在实际工程中表现为,减小支承刚度可以使临界转速显著降低。
(4)组合转子对临界转速的影响
转子系统经常是由多个转子组合而成的,例如在汽轮发电机组中,有高、中、低压汽轮机转子、发电机和励磁机转子等。每个转子都有其自身的临界转速,组合成一个多跨转子系统后,整个组合转子系统也有其自身的临界转速。组合转子与单个转子的临界转速间既有区别又有联系,其间存在一定规律。如果各单个转子是由不同制造厂生产的,那么当制造厂给出各单个转子的临界转速后,利用这一规律,就可以估计组合后转子临界转速的分布情况。此外也可估算出在组合转子的每一阶主振型中,哪一个转子的振动特别显著。
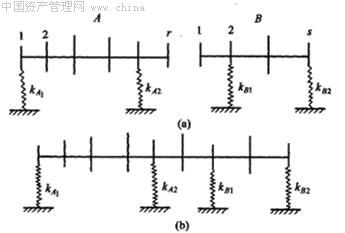
图1-7 组合转子系统
图1-7(a)为A、B两个系统,图(b)为将其刚性连接。
理论推导证明,组合系统中各转子的各阶临界角速度,总是高于原系统相应的各阶临界角速度。如图1-8所示。

图1-8 组合系统的临界角速度
|


