马晓旭 张传利 夏明超 黄益庄
清华大学电机系, 北京 100084
0 引言
随着高压远距离输电在电力系统中的应用越来越广泛,大容量变压器的应用日益增多,对变压器保护的可靠性、快速性都提出了更高的要求。当前变压器保护的主要矛盾仍集中在鉴别励磁涌流和内部故障上。对于励磁涌流,保护应不动作;对于内部故障,保护应迅速动作。
目前励磁涌流鉴别的方法大致可以分为波形特征识别、谐波识别、磁通特征识别、等值电路法[1]。在波形特征识别法中曾提出过间断角原理,近来在此基础上又引入智能化方法(如模糊判据、人工神经网络)[2,3]和小波分析方法[4],在一定程度上取得了成功的结果。这些方法均依赖于涌流波形在时间轴上间断或者畸变部分的数学特征的提取,尽管这部分畸变特征是两者的主要区别,但是这些畸变特征在复杂的实际运行情况下变得不理想,因此仅利用畸变特征的数学化参数不能可靠地区分涌流和故障波形,同时存在比较复杂的定值整定问题。其他方法也有各自的优点和局限性。
鉴于此,本文提出一种基于离散隐马尔科夫模型(discrete hidden Markov model,缩写为D-HMM)的励磁涌流的波形识别方法。由于该方法完整地利用两者波形在负半周的全部采样数据,以概率特征表述两种波形的差别,而不局限于涌流波形和故障波形在某个特征参数(如间断角)上的不同,因此可以在训练得到的模型中综合地反映两者的区别,从而可靠地动作。同时由于计算量相对较小,该方法可满足变压器保护快速性的要求。而且出口判据为输入波形采样数据在两种模型下概率的相对大小,避免了复杂的定值整定问题。数字仿真实验的结果说明本方法可很好地鉴别励磁涌流和内部故障。
1 隐马尔科夫模型
隐马尔科夫模型(hidden Markov model,缩写为HMM)的提出最初是在语音处理领域。HMM是在Markov链的基础上发展起来的一种统计模型。由于实际问题比Markov链模型所描述的更为复杂,因此在HMM中观察到的事件与状态并不是一一对应,而是与每个状态的一组概率分布相联系。它是一个双重随机过程,其中之一是Markov链,描述状态的转移;另一个描述每个状态和观察值之间的统计对应关系。这样,HMM以概率模型描述观察值序列,具有很好的数学结构,能够比较完整地表达观察值序列的特征[5]。图1是一个离散HMM(D-HMM)的例子。
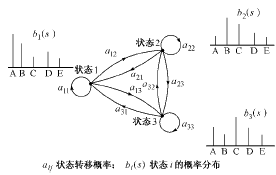
图1 离散隐马尔科夫模型
Fig.1 Discrete HMM
HMM可以记为:λ=(N,M,π,A,B),其中N为模型中Markov链状态数目;M为每个状态对应的可能的观察值数目;π为初始状态概率矢量;A为状态转移概率矩阵;B为观察值概率矩阵。
HMM的3个基本问题也已经有了比较理想的解决方案,即前向—后向算法、Viterbi算法和Baum—Welch算法(训练算法),同时提出了多观察值序列的训练算法、比例因子算法等改进方法,这为HMM的实际应用打下了坚实的基础。
2 用于涌流识别的观察值序列和训练序列
变压器内部故障时将产生高于额定电流几倍至十几倍的故障电流,基本的波形是一个含有衰减直流分量的交流正弦波。而变压器合闸时产生的励磁涌流在数值大小上接近甚至超过故障电流,两者在数值上不可区分。理论上的励磁涌流波形有明显的间断,但是由于检测电流互感器(TA)二次侧的饱和作用,涌流的间断部分将变得连续,使得间断角原理失效。尽管如此,涌流波形还是与故障波形有很大区别:涌流波形在过零处有畸变,正负半周不对称。这成为许多判据的基础。
这里,HMM的观察值序列就是变压器内部故障和励磁涌流采样数据。图2、图3是用EMTP仿真的波形。
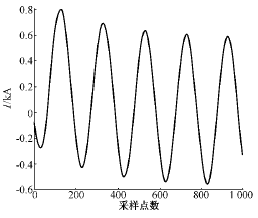
图2 变压器内部故障波形
Fig.2 Waveform of internal fault current

图3 变压器励磁涌流波形
Fig.3 Waveform of magnetizing inrush current
由于故障波形和涌流波形主要差别集中在负半周,因此HMM的训练序列采用归一化后波形的负半周。这样既可以突出两者的差别,也减少了计算量。图4、图5是两者归一化后一个负半周的波形。
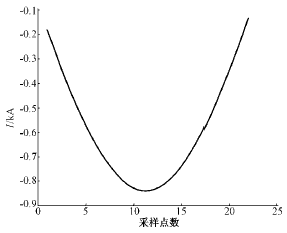
图4 故障波形的负半周
Fig.4 Negative half-cycle of fault current
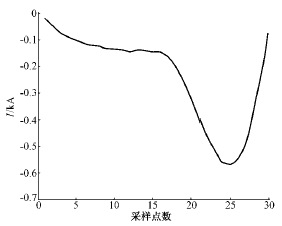
图5 涌流波形的负半周
Fig.5 Negative half-cycle of inrush current
为使得训练生成的模型能够充分反映两者波形的差别,这里将每一个负半周的采样序列作为一个训练序列,得到4个训练序列,应用多训练序列的算法进行训练。
3 离散HMM的应用
3.1 模型参数的选择
HMM最初是为语音信号处理提出的[6]。这里要处理的波形相对于语音信号而言要简单得多,因此HMM参数的选择就要相对简单,而且具有比较明确的物理含义。
由于每周期采样50点,负半周采样25点,因此首先将状态数目确定为N=25/2≈12。这样每个状态基本上对应于正弦波负半周上的均匀采样值,各状态的中心采样点的分布如图6所示。
图6 离散HMM各状态的中心采样值
Fig.6 Center of each state of discrete HMM
每个状态的可能取值为所有上述均匀采样点加上0点,但中心采样点的概率占优。由此,M=N+1,B为N×(N+1)的矩阵,B矩阵的初值用以下方法确定:每个状态的中心采样点的概率最大,其前后3个点的概率依次减小,其余采样点的概率为0。如图7所示。
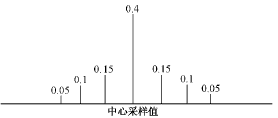
图7 B矩阵(行)初值
Fig.7 Initial value of matrix B(row)
对于A矩阵和π矩阵的初值则采用一般的均匀分布。对于状态驻留问题,由于考虑状态驻留时间的HMM的提出主要是为描述语音信号的短时平稳性,而不能采用状态驻留概率为负指数分布的一般HMM。但这里的两种信号的状态驻留基本上满足负指数分布,因此不需要应用考虑状态驻留时间的HMM。
3.2 模型的训练
这里采用的是多训练序列的HMM训练。多训练序列的训练公式为[5,6]:

其中 α*(l)t,β*(l)t分别为第l个训练序列经过比例因子处理的前向、后向变量;N为状态数;M为每状态可能的观察值数,这里M=N+1;T为训练序列的数目;O为观察值序列;φ为比例因子序列;V即上述正弦波负半周的均匀采样序列。
需要说明的是在B矩阵参数的训练时,Ot=Vk将如下处理:当Vk≤Ot≤Vk+1时,判为Ot=Vk。
3.3 实验结果
3.3.1 训练生成模型的分析
故障数据训练生成的π,A故障,B故障如下,B故障,A故障图和等高线图分别如图8~图11。
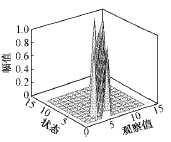
图8 故障模型B矩阵图
Fig.8 Matrix B of fault model
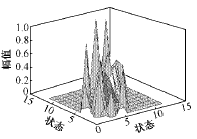
图9 故障模型A矩阵图
Fig.9 Matrix A of fault model
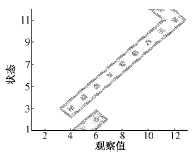
图10 故障模型B矩阵等高线图
Fig.10 Contour of matrix B of fault model
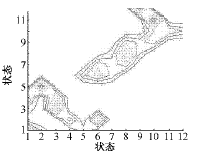
图11 故障模型A矩阵等高线图
Fig.11 Contour of matrix A of fault model


由B故障可看出,因训练数据范围为0~-0.9,所以在任何状态中V的前3个采样值和最后1个采样值(即0)的概率都是0,而且每个状态基本上对应V的一个采样值,即中心采样值,其余采样值的概率基本为0。同时,可以看到状态1、状态4,状态2、状态5的概率分布分别相同,为同一状态。而状态10、状态12也基本为同一状态。
在分析B故障的基础上,可以看到A故障中各状态向左、右两相邻状态的转移概率基本上是相同的,这与故障波形的对称性相符合。
涌流数据训练生成的π,A涌流,B涌流如下,B涌流,A涌流的等高线图分别如图12、图13。

图12 涌流模型B矩阵等高线图
Fig.12 Contour of matrix B of inrush model
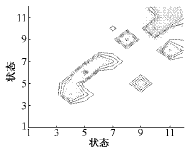
图13 涌流模型A矩阵等高线图
Fig.13 Contour of matrix A of inrush model


由B涌流可看出,因训练数据范围为0~-0.7,所以在任何状态中V的前7个采样值和最后1个采样值(即0)的概率都是0,而且每个状态也有一个中心采样值。同时在表达涌流波形时所需要的状态数不多,所以前3个状态的概率分布为全0。状态5、状态6,状态7、状态9,状态11、状态12分别为同一状态。
在分析B涌流的基础上,可以看到A涌流在状态10、状态11(12)处有明显的高驻留概率,这与前面涌流波形也是一致的。这一点从等高线图上也可以看出。
3.3.2 涌流和故障识别
在训练得到的模型基础上,应用前面故障和涌流的第1个归一化负半周的数据作为检验数据,结果如表1所示。
表1 应用离散HMM识别结果
Table 1 Result of inrush identification using discrete HMM
检验数据
故障模型
涌流模型
两者之差
故障数据
-6.5265
-138.6899
132.1634
涌流数据
-50.3383
-4.6770
[1] [2] 下一页
|


