1  引言
    风力发电是近一二十年来逐步发展起来的一种新型环保发电方式。它没有燃料的加热过程，不会向大气层排放任何有害气体，对减弱温室效应和减少环境污染能起到积极的作用。同时它还具有安装方便、操作简单、启停速度快和运行维护费用低等优点。因此，风力发电已成为可再生能源中发展最快的一种发电方式，目前已经形成商业化运营的规模。到2000年底，我国已建成并网风力发电场26座，总装机容量超过340MW。预计到2005年将达到全国电力总装机容量的0.3%，即1200MW左右。在未来的几十年中，风力发电还将有更大的发展。
    然而，风力发电会对电力系统的运行产生一定影响。如：
    1）风力发电机是以风作为动力的，其输出特性会直接受风的影响。风的随机波动性和间歇性决定了风力发电机的有功功率也是波动的和间歇的。
    2）风力发电机是一种异步发电机，在其发出有功功率的同时还要从系统中吸收无功功率。
    当风电场的容量较小时，这些特性对电力系统的影响并不明显。随着风电场容量在系统中所占比例的增加，风力发电对系统的影响就会越来越明显。大风速扰动会使系统的电压和频率产生很大的变化，严重时将可能使系统失去稳定。另外，风电机组的运行受致于系统的运行条件，当系统运行条件比较恶劣，如电压水平比较低时，风电机组就很容易在系统扰动或风速波动下停机，从而使系统造成有功缺额，不仅给风电场带来经济损失，也可能使系统失去稳定。为了描述某一电力系统中能够承受的风电场容量，因而引入了风电场穿透功率极限的概念。
    风电场穿透功率是指风电场装机容量占系统总负荷的比例。风电场穿透功率极限定义为接入系统的最大风电场装机容量与系统最大负荷的百分比^[1]。即

    风电场并网容量的增加会引起系统的电压和频率产生偏差、电压发生波动和闪变，以及电压稳定性受到影响等问题，而且系统为减小风电场发电间歇性对系统的影响而必须增加旋转备用容量，从而使系统的可靠性和经济性下降。因此计算风电场穿透功率极限非常重要。但由于涉及的因素较多，范围较广，至今还没有统一的算法和公式。一些欧洲国家在计算风电场穿透功率极限方面进行了许多工作，积累了不少经验，但由于这些国家的电网结构紧密，因而在计算过程中都不考虑电力系统暂态稳定问题。文献[2]～[4]分别从系统频率偏差、稳态电压水平、总谐波畸变率等方面对风电场穿透功率极限进行了计算。文献[5]分析了风电场可靠性对风电场穿透功率极限的影响。文献[6]在优化计算风电场穿透功率极限中考虑了系统的静态安全约束。
    我国电网结构薄弱，风电场的地理位置一般距负荷中心较远，所以在计算风电场穿透功率极限时必须考虑风电场的暂态稳定性。本文提出了基于系统暂态稳定性分析的风电场穿透功率极限的计算方法，应用中国电力科学研究院的电力系统综合分析程序(PSASP)中的用户接口程序(UPI)对风电场并网运行进行了动态仿真，并用实例计算了在一定条件和判据下的风电场穿透功率极限。
2  风力发电机组动态数学模型
    风力发电机组动态数学模型由动力系统和异步发电机构成，其能量流程如图1所示。风电机组通过动力系统将风能转换为机械能，进而由异步发电机转化为电能。风电机的动力系统可用代数和微分方程来描述^[7]，异步发电机可采用3阶微分方程表示^[8]。

2.1 风电机组动力系统数学模型
    风力发电机动力系统的数学模型可表示为

式中 M_w为风力机叶片转矩；ρ为空气密度；C_p为叶片风能转换效率系数；R为叶片扫风半径；λ为叶尖速率比；Ω为叶片机械角速度；Ω_N为叶片额定机械角速度；P_N为风力发电机组输出的额定功率；v_w为作用于风力机的风速；M_h为轮毂侧转矩；M_w为叶片侧转矩；T_h为轮毂惯性时间常数；M_t为联轴器齿轮箱侧转矩；M_mg为联轴器发电机侧转矩；T_t为齿轮箱和联轴器的惯性时间常数。 
2.2  异步发电机数学模型

式中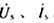和r₁分别为异步发电机定子的电压、电流和电阻；x₁、x₂和x_m分别为异步发电机定子漏抗、转子漏抗和激磁电抗；为异步发电机暂态电势；为定子绕组开路时转子绕组的时间常数；s为异步发电机滑差；M_m和M_s分别为异步发电机机械转矩和电磁转矩；T_j为异步发电机惯性时间常数；Re(·)为取实部；的共轭。
3  风电场穿透功率极限计算方法
    通过分析系统暂态稳定性来计算风电场穿透功率极限时要综合考虑系统运行方式、扰动方式、风电机组自身保护以及稳定判据等因素的影响。
3.1  系统运行方式
    对于含风电场的电力系统而言，在以下2种运行方式下风电场的并网运行对系统运行的冲击最大，只要在这2种运行方式下能够保证系统稳定，就可以保证系统在其它运行方式下也能稳定运行。
   （1）系统负荷最大。在这种情况下，系统热备用较少。如果在很短的时间内风速由额定值减小至零风速，则风电场的有功功率会在短时间内由最大输出功率降为零；如果此时热备用发电容量较少，有功缺额将使系统频率和电压产生大的变化。
    （2）系统负荷最小。在这种情况下，风速如果在很短时间内由零风速增至额定风速，风电场的有功功率将会在短时间内由零增加到最大输出功率，此时若发电机有功调节能力较差，则系统中产生的有功增量将对系统的稳定运行产生较大影响。
3.2  扰动方式
    在进行暂稳计算中采用3种扰动方式：
    1）N-1故障。故障类型为发电厂1回出线考虑故障重合闸的单相永久接地短路故障。
    2）风速扰动1。风速在短时间内由停机风速升至额定风速。
    3）风速扰动2。风速在短时间内由额定风速降至停机风速。
    风电场风速的变化模式是按最剧烈的变化模式来考虑的，即假设风电场内各个风机处的风速变化是一致的，且不考虑尾流效应，则风速在5s内可以从零上升到额定风速，或由额定风速降至停机风速。
3.3  风电机组保护
    计算中考虑了风电机组内部的电压保护。当机端电压高于额定电压10%且超过100ms，或高于额定电压6%且超过60s，或低于额定电压15%且超过400ms，或低于额定电压10%且超过60s时，发电机将自动停机。
3.4  稳定判据
    1）在本文的计算中，系统发生故障的稳定判据为系统中发电机最大功角差不超过180º，各节点电压低于0.85时不超过0.8s，则判为稳定。
    2）风电场正常运行时风速是波动的，因此系统各节点电压和频率也随之波动。当各节点电压偏差在额定值的±10%内和频率偏差在±0.5Hz内时，则为稳定运行。
3.5  计算步骤
    在每1种运行方式下的计算步骤如下：
    ① 给定初始状态；
    ② 计算系统故障情况下保证系统稳定的风电场发电功率临界值P₁；
    ③ 计算2种风速扰动情况下保证系统稳定的风电场发电功率临界值P₂和P₃；
    通过计算得到2种运行方式下的6个功率临界值，其中最小的就是所要求的风电场穿透功率极限。
4  算例分析
    算例系统主接线如图2所示。该系统中发电厂总装机容量为1948.9MW，其中水电装机容量为103MW，火电装机容量为1788.4MW，风电装机容量为57.5MW。由于水电所占比例较小，所以系统功率调节能力较差。风力发电场(节点编号为1)通过110kV双回线路与节点8相连，风电容量较集中且在系统中所占比例较大。应用本文提出的计算方法，计算了该系统在节点1处的风电场穿透功率极限。

计算工具采用PSASP，风电场模型用UPI。系统中常规发电机组采用E′q变化模型。为考虑调速器作用，负荷均采用50%感应电动机模型和50%恒阻抗模型。    
　 计算中扰动方式为：
    　1）系统故障。线路1-8的节点8侧发生单相永久性故障，0.14s后故障相断开，1s后故障相重合于故障，0.14s后故障线路三相断开。
    　2）风速扰动1。风速在短时间内由停机风速升至额定风速。
    　3）风速扰动2。风速在短时间内由额定风速降至停机风速。
  系统运行方式分别考虑了冬季大负荷方式和夏季小负荷方式。
  　（1）冬季大负荷运行方式下的稳定性分析。
　　在该运行方式下系统总负荷为1240MW，功率因数为0.9，除风电场外其他发电厂的总有功功率为1168MW。考虑系统故障和风速扰动情况下的计算结果如表1所示。

   （2）夏季小负荷运行方式下的稳定性分析。
    在该运行方式下系统总负荷为670MW，功率因数为0.9，除风电场外其他发电厂的总有功功率为635MW。考虑系统故障和风速扰动情况下的计算结果如表2所示。

[1] [2] 下一页