1　引言
　　发输电组合电力系统涉及的设备种类多，结构及运行方式复杂，故障模式往往是重叠的或相关的，它是电力系统的主体部分，对负荷点的供电可靠性有极为重要的影响。组合系统可靠性被认为是可靠性领域中最重要、但又研究最少的问题之一。
　　解析法由于其计算量随元件数增加而剧增，处理相关故障模式比较困难，因而在复杂系统的分析中应用有限^［1～4］。蒙特卡罗模拟为解决这类问题提供了另一条可供选择的途径，在处理故障相关性、节点负荷间的相关性以及预测不确定性、电气设备的动作顺序及逻辑关系等方面有独到之处。本文在发输电组合系统可靠性模拟算法的框架结构及实现方面作了研究，算例验证了模型的可行性和合理性。

2　元件模型及算法实现
2．1　发电机组模型
　　发电机组的故障被认为是彼此独立的。对一台有N_g个出力状态的发电机组可用两个1维数组来描述，C＝｛c_i｝、P＝｛p_i｝，其中c_i、p_i分别为机组的出力值及概率。定义：

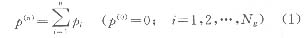
　　抽取一均匀分布的随机变量u，当u满足p^（n－1）＜u≤p^（n）时，认为该发电机在发电状态c_n。上述抽取过程对每台发电机顺序进行。
2．2　负荷模型

2．2．1　年峰荷模型
　　以年最大负荷出现时刻为基准，不考虑负荷的变化，所得的风险指标称为年度化（annualized）指标。各节点负荷与系统负荷间存在的比例关系为　　

式中　K_j为比例系数；L为系统总负荷；N_L为负荷节点数。
　　显然节点负荷间是完全相关的。对负荷预测的不确定性，可用一正态分布随机变量L～N（L，σ²）表示。其中σ为预测标准差，由计算人员给定。利用正态分布抽样技术，可以确定系统总负荷值，然后用式（2）分配到各节点去。
2．2．2　分级负荷模型
　　利用电力部门提供的统计数据和典型日负荷、月负荷和年峰荷模型可形成全年8760h负荷，在此基础上可将数值相同的负荷合并，形成n≤8760个分级负荷。

2．3　输电线路模型

2．3．1　独立故障
　　考虑输电线路故障有3种故障模式：开路、瞬时性短路和永久性短路。具有相同故障后果的继电保护故障、断路器故障也已合并考虑^［5］。
　　假设开路故障（包括断线、保护误动、常闭断路器误分）概率为p_o，瞬时性短路故障概率p_i，永久性短路故障（包括线路短路、断路器线路侧可自动清除的故障）概率为p_s，则当0＜u≤（p_o＋p_i＋p_s）时，该线路发生故障。
　　可进一步判断：当0＜u≤p_o时，线路发生开路；当p_o＜u≤（p_o＋p_i）时，线路发生瞬时性短路；当（p_o＋p_i）＜u≤（p_o＋p_i＋p_s）时，线路发生永久性短路。
2．3．2　相关故障
　　设线路i的故障与另外m条线路的故障相关，i线故障后j线故障的概率为p_ij，则可以用一矩阵来描述这一概率相关关系：P＝［p_ij］_m×m　（0≤p_ij≤1．0）（3）　　

    实际系统中，m的值并不大。需注意的是一般情况下p_ij≠p_ji。
　　模拟过程中，当线路i故障后，针对P中的第i行元素p_ij（j＝1，2，…，m），抽取m个均匀分布随机变量u_k（k＝1，2，…，m），当u_k≤p_ik时，则第k条线发生相关故障。
2．3．3　共同模式故障
　　共同模式故障是指由于同一原因使多个元件同时故障。令n条线路发生共同模式故障的概率为p_c，当u≤p_c时，则n条线同时发生故障。
2．4　母线模型
　　母线故障包括母线永久性短路、断路器母线侧可自行清除的故障。设故障概率为p^bus_s，抽取u～u（0，1），则当u≤p^bus_s时，该母线发生故障。母线故障将使连在该母线上的所有线路全部跳闸。
2．5　变压器模型
　　变压器模型与发电机模型类似，可用相同方法处理，最常用的是两状态模型。
2．6　断路器模型
2．6．1　常闭断路器拒分
　　令断路器拒动和继电保护拒动的概率分别为p^B_f和p^R_f，抽取u～u（0，1），则
当u≤（p^B_f＋p^R_f）时，继电保护系统拒动；当u≤p^B_f时，断路器拒动；
当p^B_f＜u≤（p^B_f＋p^R_f）时，属继电保护拒动。
　　进一步区分是断路器还是保护拒动的目的在于确定后备保护的动作范围。在这两种情况下，后备保护的动作范围不一样，故障涉及面不同。
2．6．2　常开断路器拒合
　　令断路器拒合概率为p^B_r，抽取u～u（0，1），则当u≤（p^B_f＋p^R_f）时，断路器拒合。拒合常出现在分段开关、母联开关或以旁路开关代替出线开关的情况。
2．7　重合闸模型
　　令重合闸拒动的概率为p^Y_f，当u～u（0，1）≤（p^B_f＋p^Y_f）时，认为重合闸拒动，线路的瞬时性故障转化为永久性故障。后果与线路开路相同。只有在发生瞬时性故障的前提下才考虑重合闸拒合。
3　系统分析模型
3．1　基态情况下的安全经济分配模型
　　目的是在系统正常运行方式下确定每台发电机的输出功率及线路上的潮流分布。采用考虑N安全
性线性规划模型，目标函数为系统发电成本最低：

式中　b_i、GF_i为第i台发电机的平均生产成本和发电功率；GF^max_i、GF^min_i为发电功率上下限；T_ij、T^max_ij为线路有功潮流及有功上限；D_i为节点有功负荷。
　　线路潮流采用直流潮流法计算。模型将输出每台发电机的发电功率及状态（冷备用或旋转备用或满载）和每条线路上的初始潮流。
3．2　网络拓扑分析
　　采用前述方法对系统中每个元件进行抽样和事故后果分析后，受影响的发电机、变压器、母线和线路均已切除，网络拓扑与初始状态相比有了变化，需重新进行连通性分析以输出电网连通块数（孤岛数）以及每个连通块内的发电机、负荷和线路连接情况。

　　所采用的方法为顶点融合法。以母线为节点，以线路、断路器、变压器为边进行搜索。当两个顶点间有一条边时，两个顶点合并，每个连通块最后都各自合并为一个顶点。连通性搜索分两个层次进行：变电站内搜索是确定计算节点的个数，断路器的开闭将导致节点分裂或合并；输电网搜索是确定需进行潮流计算的孤岛数。
　　3．3　安全分析

　　计算节点的有功发生变化或线路开断后，需进行安全分析以判定线路有功及无功潮流是否越界。若越界，则将统计各线路的最大过负荷量和线路过负荷概率等，以找出网络的薄弱环节。
　　蒙特卡罗模拟可计入任意多重发电机和线路故障，目前软件设计中采用了基于直流潮流和交流潮流的安全分析算法。安全分析时，根据不同的要求采用相应的有效算法。
3．4　有功校正和发电再调度
　　有功校正和发电再调度的目的是消除线路过载，并使发电总功率和负荷总需求保持平衡。以有功切负荷量最小为目标的线性规划模型为_［6］

　式中　DF_i为节点i的切负荷矢量。
　　实际应用中，有功校正模型还可进一步考虑：①有功缺额时低频减载的影响；②切负荷节点距故障节点的距离；③切负荷所造成的停电损失费用；④发电成本的影响等因素。
4　算例和讨论
　　计算用例系统数据取自文献［7］，其电气接线图见图1。限于篇幅，例系统数据从略。在以下的结果比较中选取了3个有代表性的风险指标进行分析，即：停电概率（LOLP）、停电电量（EENS）、最大切负荷功率（X_max）。
　　为了讨论不同元件故障模式对系统和节点可靠性指标的影响，设计了以下计算方案：
    方案一：只考虑发电机和线路独立故障；
　　方案二：在方案一基础上考虑线路2、6之间和线路3、7之间的共同模式故障；
　　方案三：在方案一基础上考虑保护系统故障（即断路器绝缘故障、继电保护装置和自动重合闸拒动故障），拒动概率为0．01；
    方案四：在方案一基础上考虑母线段故障；

　　方案五：同时考虑线路3、7之间、线路2、6之间的共同模式故障和发电机、变压器、保护系统、母线段故障。
    上述方案的切负荷策略均以最小切负荷量为目标函数，每个方案随机抽样5万次，在586／133微机上平均计算时间约为1min20s。各方案选择了具有代表性的指标汇总于表1和表2。为了比较，表1中最后栏列出了参考文献［7］提供的部分结果。对这些结果讨论如下：

                        
　　                         图1　系统接线图　　
　　（1）在考虑全部故障模式的条件下（方案五），本文提供的系统风险指标大于文献［7］所提供的指标。这是因为在文献［7］中只考虑了两重故障（两机、两线或一机一线），对高阶故障忽略不计，一些更为严重的故障状态未予考虑，故结果偏小。各节点指标的差异在于采用的切负荷策略不同，文献［7］只考虑在与故障元件直接相连的负荷点切负荷，而本文的结果是以全系统切负荷量最小为目标函数，切负荷地点及数量由线性规划求出。以节点2和5为例，文献［7］中节点2 EENS偏大，而节点5 EENS偏小，是因为节点2中7台发电机的任意一台发生故障均会导致节点2切负荷，而发电机的故障概率相对较大，故节点2的切负荷量较大，节点5切负荷量较小（是因为它仅当输电线路故障时才会切负荷，而输电线路的故障概率相对较小，故其切负荷的可能性也较小）。节点6切负荷量较大是一个例外，因为它是单线供电，一旦线路9发生故障必将断电。
　　（2）从表1还可见，不同故障模式对系统和节点可靠性指标影响程度是不同的。以节点4为例，其LOLP指标在母线故障下变化不大，但其EENS指标变化很明显。即在切负荷次数基本相同的情况下切负荷量大幅度增加。节点5在各种故障情况下的LOLP和EENS同步增长，这种现象的出现与系统的网络结线、变电站内部结构、切负荷策略等因素都有关。就系统LOLP指标而言，影响较大的故障仪次是母线故障、保护系统故障和共同模式故障，而对系统EENS指标影响较大的故障依次是母线故障、保护系统故障和共同模式故障。这些结果表明：所采用评价指标不同，为改善这些指标所采用的措施也不同，对系统各部分（负荷点）的影响也不同。
　　（3）从表2可见，在方案一基础上考虑各种故障后，输电网元件停运造成的停电量比例均有不同程度上升。单项故障中上升较多的是母线故障和保护系统故障，因为这两种故障都可能导致多条线路或多个断路器断开。同时考虑多种故障后，方案五的指标也并不是各单项故障下相应指标的简单叠加，因为它们之间存在重叠现象，但总趋势是增加的。

　　表1　不同故障模式下计算结果比较

表2  各类元件故障引起的停电量及其占系统停电量的比例

5　结语

    本文提出的发输组合系统可靠性评估采用蒙特卡罗仿真模型和算法是合理的、可行的。相应的计算分析软件已达到实用水平，并已在安徽电网的规划及可靠性评估中应用，所得结果为电网的合理建设提供了有价值的参考意见