尤海波 刘笙
上海交通大学电力系,200030 上海
1 引言
最近10年,电力系统的能量管理系统(EMS)已具备静态安全分析(SSA)功能,但是在线动态安全评定(DSA)的进展很小,主要的问题是计算速度。DSA的目的是决定哪些偶然事故将导致系统不稳定或电压跌落越限。在现今的实践中,运行方式组在少数典型情况下进行离线研究,其结果作为调度员的导引而实施,由于实际运行情况难以与上述典型情况相吻合,因而采用保守的极限,而保守的极限往往会造成不经济的送电。直接暂态稳定分析的暂态能量函数(TEF)方法植根于现代动力系统稳定理论之中,具有估价稳定程度的定量性与计算快速性的独特优势,因而成为在线稳定分析的主要候选方法。
TEF方法的可靠性仍是当今人们关注的焦点,没有足够的可靠性就难以发挥其快速性。决定可靠性的关键一环是体现稳定域边界性质的临界能量,由此TEF方法可分为位能边界曲面(PEBS)方法[1]与主导不稳定平衡点(CUEP)方法[2]。PEBS方法几乎不受模型限制,且计算快速。在故障的电厂模式下快速有效,而在网络中发生故障或非临界机具有内部振荡时有时会导致保守的或冒进的估计。当今受到关注的CUEP方法是基于稳定域边界理论的主导不稳定平衡点(BCU)方法[3],在稳定域估计时,具有偏保守性质。对故障的电厂模式和区域模式,通常均有效,但在高维状态空间中求解CUEP并不是一件轻松的工作。不同的系统需要协调计算参数,工作量大致高出PEBS方法一倍以上,但当它运用于非机端故障下的稳定评估时,可以避免冒进的结果。本文是在PEBS方法及BCU方法改进成果的基础之上提出一种两者优势互补的稳定评定方法,即以故障点是否发生在机端为标记,分别运用PEBS方法及BCU方法作为动态安全分析中偶然事故的分类器,可以显著提高直接法的可靠性及计算速度。值得指出的是文[4]也是运用不同的直接法进行综合分析的。但文[4]对RUEP是用MOD方法,本文用BCU方法,此外文[4]用“容错表决”方法,本文提出以机端故障为标记的一贯分类特征,并为此阐明了这种分类器的物理依据。
2 PEBS方法的改进
多机系统的动态稳定域可用角度子空间中等位能曲面族形成的位能“钵体”表示。图1表示三机系统的三维位能“钵体”[1]。事故后的SEP处于钵底,UEP围绕SEP处于“钵体”的“脊”上,称为PEBS。若运动中的系统故障轨线越过“脊”达到不稳定,则表示系统失去同步。在临界不稳定的情况下,事故后系统的轨线将在一点接近于某UEP,称为CUEP,滑出“脊”达到不稳定,如图2[1]。数学上表征PEBS的经典方法是从事故后的SEP沿任意方向发出的射线达到局部位能最大值的点。由于射线是全方位的,因而该点集能够形成PEBS。
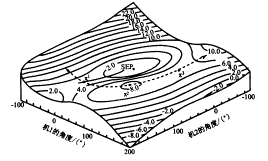
图1 三机系统的等位能曲面及PEBS
Fig.1 Equi-potential energy surface
and the PEBS for 3-machine system
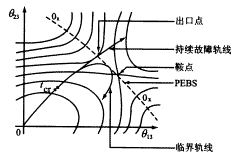
图2 临界的和持续的故障轨线的PEBS穿越点
Fig.2 PEBS crossing of critical
and sustained fault trajectories
PEBS方法是以持续故障轨线(代替临界故障轨线)在角度空间的投影上寻找达到事故后系统的PEBS的出口点(EP),其判别式是[5]
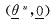 (1) (1)
式中 fi为附录中式(A2)的右端式的分量,属于事故后的结构;θsi为事故后系统稳定平衡点的分量;m为系统发电机数。
以出口点处的恒值能量曲面近似局部稳定边界[1]。因而临界能量由下式表示
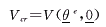 (2) (2)
式中 θe为PEBS的出口点。
判别式(1)对于故障的电厂模式快速有效,在网络发生轻微故障或重故障时,有时会产生误判。在轻微故障下,会产生小的摇摆振荡,发生无关的局部位能最大值,形成悲观估计。在重故障下,当VPE达到maxVPE时发电机转子功角已远大于180,形成过分乐观的估计,因而需要检测发电机转子角度以作为补充判据:
(1)若系统位能VPE在180。>θmax>90。的范围内抵达maxVPE,则用标准判别方式;
(2)若VPE在θmax<90。时抵达maxVPE,则宣布属于高稳定情况;
(3)若VPE在抵达maxVPE时,θmax已远大于180。,则宣布属于很不稳定情况。
3 BCU的改进方法
BCU方法是建立在现代非线性动力学系统理论基础上的一分析方法。文[3]导出了事故后稳定平衡点吸引域的完全拓扑特征,并将该稳定域边界规定为不稳定平衡点的稳定流形的并集,起始于事故前SEP的故障时轨线遇上稳定边界上的一点,称为出口点(EP)。特定故障下的UEP简称CUEP,其稳定流形包含故障时轨线的出口点。通常决定临界不稳定轨线的出口点(亦称动态逸出点DLP)非常困难,而SEP及UEP的流形无显式表示。若用一能量函数代替UEP的稳定流形,则工作较易进行,因此可以说CUEP方法是用CUEP的恒值能量面去近似逸出点(DLP)的方法。BCU方法也是PEBS方法与CUEP方法的有效结合[3],见图3。
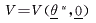 (3) (3)
式中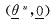 是CUEP。 是CUEP。
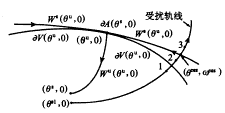
图3 BCU方法[3]
Fig.3 BCU method
因为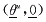 的稳定流形Ws 的稳定流形Ws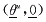 上任意点的能量函数值总是大于或等于常值能量面V 上任意点的能量函数值总是大于或等于常值能量面V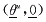
上的值,从而实际上保证了故障时轨线在穿过Ws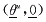 之前先穿过常值能量面V 之前先穿过常值能量面V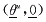 。这也说明了BCU方法的偏保守性质。当原始系统的转移电导Gij足够小时,运用原始系统和梯度系统的相关性质,求取CUEP。其基本步骤如下[3,6]: 。这也说明了BCU方法的偏保守性质。当原始系统的转移电导Gij足够小时,运用原始系统和梯度系统的相关性质,求取CUEP。其基本步骤如下[3,6]:
①计算持续故障轨线在角度空间的投影,直至与事故后梯度系统的稳定边界相交,该交点称为出口点(EP),可运用变阶变步长的隐式Adams方法求解故障时轨线及EP;
②以EP为初值,积分事故后梯度系统,直至一最小梯度点(MGP),由于梯度系统的刚性,可运用变阶变步长的Gear法或BDF方法求解;
③以MGP为初值,用牛顿法迭代求解转矩平衡方程和网络方程,得到CUEP。
对于一般电力系统模型,在高维状态空间中求取CUEP并非易事,有可能找不到MGP,从而导致系统发散或收敛到邻近的SEP,或者虽然找到MGP,但收敛到错误的UEP。在出现这些情况时,可运用一种校正梯度系统积分轨线的方法,称为阴影方法[4],如图4所示。其基本思想是,当梯度系统积分轨线偏离PEBS时,每隔四五步,运用点积判据(1)校正,将其拉回PEBS,可以取得显著效果。具体步骤如下(代替上述步②,③):
①以θmi (i=0,1,2,…,N)为初值积分梯度系统5步得到点θri。θm0取出口点值;
② 搜索射线R(θri) ={θ∶θ=(θri-θs)α+θs,α≥0}上的点,直至找到点θri 满足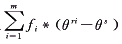 =0,则θm(i+1)=θri ,转步①。 =0,则θm(i+1)=θri ,转步①。
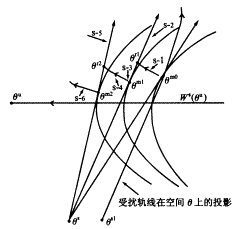
图4 阴影方法
Fig.4 The shadowing method
在应用该方法时并不能预先确定N值,而是在过程中通过准则检定。该准则是测点距离平衡点的量度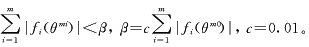
4 在线DSA中的TEF分类器
由前述可见,在机端发生故障情况下,采用PEBS方法判别稳定性,既保证可靠判别,且比BCU方法节约一半以上时间;在网中发生故障时采用BCU方法分析,则可保证可靠判别,虽然稍为保守,但避免了冒进的结果。因此,本文提出的PEBS/BCU分类器是以故障是否发生在机端为标记的。
机端故障与非机端故障的本质区别在于前者在两群模式下群内严格同调,并表现为首摆失稳。这时PEBS属常态边界,且持续故障轨线与临界故障轨线相当接近,这时持续故障轨线总是先穿过出口点的常值能量面,而后穿过CUEP的稳定流形,因而用PEBS方法有效。当网中(非机端)发生故障,特别是出现非临界机内部振荡时,PEBS畸变为病态边界,且持续故障轨线与临界故障轨线相距甚远,持续故障轨线可能先穿越CUEP的稳定流形,而后穿越出口点的恒值能量面,因而不能用PEBS方法判别稳定性。当用BCU方法时,由持续故障轨线求出口点只是一个导引,求CUEP才是目的。
根据以上论证,一种可靠、高效的TEF分类器可用于在线DSA中对偶然事故进行筛选、排队,其框架如图5。由第5节的实例可见,仅有极少数偶然事故需用仿真分析,因而能够有效地应对DSA中计算速度的挑战。
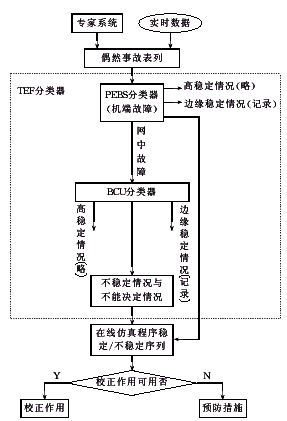
图5 在线DSA中的TEF 分类器
Fig.5 TEF classifier for online DSA
5 实例分析
为验证上述方法,用简化华东16机51节点系统[8]及中国电科院6机22节点测试系统计算临界故障清除时间。故障形式为三相短路,系统采用网络结构保持模型,以仿真程序为依据比较了PEBS法、BCU经典方法和BCU改进方法的结果,如表1及表2所列。表1中发电机用E′q代表,负荷记入电压特性。由表1可见,在机端故障下,用PEBS方法均能达到优良的结果。
表1 16机51节点系统临界清除时间
序号
故障线路
故障点
故障形式
临界清除时间/s
仿真法
PEBS方法
1
27*-45
5#机端
3LG-0
0.235~0.245
0.245
2
27*-45
5#机端
2LG-0-C-0
(0-0.16-0.35-tcs)
0.610~0.620
0.615
3
18*-19
1#机端
2L-0-C
(0-0.16-tcs)
0.285~0.295
0.291
4
18*-19
1#机端
2LG-0-C
(0-0.16-tcs)
0.230~0.240
0.236
5
18*-19
1#机端 [1] [2] [3] 下一页
|


