王力军 胡刚
湖北省电力试验研究所 湖北 武汉 430077
以往对保护装置在系统发生振荡过程中动作行为的研究,只能在动模试验室中进行,且存在投资大,建模比较费时,试验重复性、灵活性、扩充性差等缺点。随着计算机和电子技术的发展,电力系统电磁暂态数字仿真技术得到了越来越广泛的应用。
本文依据系统振荡时电气量的变化规律以及在振荡条件下对继电保护装置性能研究的需要,用数字表达式近似地模拟系统发生振荡时两侧电源频率的变化过程,并利用电磁暂态程序(EMTP)计算出振荡时电气量的变化数据。实现用数字方法仿真系统振荡过程。
1 振荡时电源频率变化的数学模型
系统振荡对保护装置的影响主要考虑的是:
(1) 振荡时电流第一次达到最大值(两侧电势相差180°)的期间,一般不小于0.4s。
(2) 振荡过程中最小振荡周期一般不小于0.1s,即两侧电源频率之差最大为10Hz。
(3) 系统最长振荡周期不大于1.5s。
对于两端电源系统来说,正常运行时,两端电源的频率均为50Hz,以一恒定的相角差运行。系统发生振荡时,对于电源为发电机时,其频率应该发生变化;电源为系统时,其频率保持不变。本文所建立的振荡模型是针对两端系统而言,在振荡发生时M端的电源频率升高,N端的电源频率降低。根据振荡的特征及考虑对保护影响研究的需要,在模型中将电源频率的变化分为3个时间段。为了简化计算,每个时间段用线性数学表达式来描述。
第1时间段描述系统稳定的破坏程度。从振荡发生开始,到两侧电源相位第一次相差180°为止,其持续时间为T1,频率变化的斜率用K1表示。
第2时间段描述振荡的严重程度。从两侧电源相位第一次相差180°开始,到两侧的电源频率之差达到最大时为止,其持续时间为T2,频率变化的斜率用K2表示。
第3时间段描述系统恢复同步的过程。从两侧的电源频率之差达到最大时开始,到两侧电源频率值均为50 Hz为止。其持续时间为T3,频率变化的斜率用K3表示。
系统振荡时,两端电源频率线性变化的数学表达式如下
fm=[1+K(t)]×50Hz
fn=[1-K(t)]×50Hz (1)
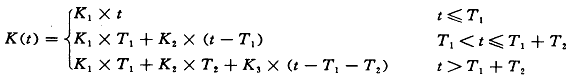 (2) (2)
根据各时间段的定义,推导出的斜率与持续时间的关系如下:
t=T1时
2π(fm-fn)×T1=π-θ(θ为初相角)(3)
t=T1+T2时
fm-fn=Δf(Δf振荡时最大频率差,Δf≤10Hz)(4)
t=T1+T2+T3时
fm=fn=50Hz
将公式(1)和(2)分别代入公式(3)、(4)、(5)中得到:
K1=(π-θ)/(220×π×T1×T1)
K2=〔(Δf/100)-K1×T1〕/T2
K3=-(K1×T1+K2×T2)/T3
在频率变化数学模型中,改变各个时间段的持续时间,就可以仿真不同的振荡曲线,从而模拟出不同的系统振荡方式。
2 系统振荡的仿真
对系统各种运行方式下的保护安装处的电流、电压暂态数据的计算是由EMTP程序来实现的。用户按照电磁暂态程序中各元件仿真的规则,填写真实系统的各组成元件的参数卡,并按真实系统的形式将各仿真元件联接成与之相对应的网络,就可以得到所需的仿真模型。在模型中不同地点,不同时间设置开关的闭合、打开,就可以模拟出系统中任意点发生的任意一种类型故障,EMTP可以计算输出网络内任意一点电气量的离散计算结果。EMTP程序本身不具有可变频率的电源模型,因此EMTP不具备直接仿真计算系统振荡的功能。但EMTP程序允许由用户自定义电源函数(每个计算步长,填写一张电源数据卡片)。依据上述所建立振荡时电源频率变化数学模型,按EMTP的计算步长计算出每一步长时刻两端电源的数值,形成符合EMTP程序自定义电源数据格式,并形成一张自定义电源卡,从而解决EMTP程序不能直接使用可变频率电源的问题,使EMTP程序能进行系统振荡的仿真计算。
EMTP程序是用数值解法来求得所模拟系统的暂态解,在使用过程中存在着稳态初始解的设定问题。保护装置(特别是微机保护装置)也要求一开始输入装置内的电压、电流量是系统的稳态值。在系统振荡模拟仿真计算时,系统两端的电源首先采用稳态交流50 Hz电压源,以满足EMTP算法及保护装置的稳态要求,然后用自定义的电压源代替交流50 Hz电压源,开始系统振荡的模拟仿真计算,从而可以得到较为满意的振荡模拟效果。
在EMTP仿真网络中,若系统两端电源采用了频率按时段线性变化的模型后,就建立了系统纯振荡的仿真模型。假定在振荡中发生故障时,系统两端的电源频率仍按时段线性变化,就可以用EMTP对任一两端系统,任何一点的各种故障进行暂态程序计算,从而得到保护安装处在各种系统振荡及振荡中又发生短路运行方式下电流、电压暂态波形数据。系统振荡模拟仿真的过程如下:
(1) 依据所需模拟的系统振荡波形变化特征,给出所需建立的振荡数学模型的各段持续时间值T1、T2、T3及振荡时最大频率差值Δf,并计算出各时间段内频率变化的斜率K1、K2、K3。
(2) 通过编写好的转换程序,按振荡时电源频率变化的数学模型,计算出两端电源在EMTP程序每个计算时刻的电压值,并按EMTP程序中自定义电源格式形成数据文件。
(3) 按照EMTP的仿真原则建立所要模拟的系统网络模型,系统两端的电源开始为交流50 Hz的电压源,经过一段时间后切换为模拟振荡时电源频率变化的自定义电压源。
(4) 将EMTP计算得到所需的电压、电流暂态数据存盘,通过已编写好的转换程序将盘中暂态数据文件转换为符合COMTRADE格式(美国电力系统暂态数据交换标准)的数据文件。
(5) 用F2250测试仪将符合COMTRADE格式的数据文件变为模拟量输出,实现对系统振荡的模拟仿真。
图1为一两端电源系统,所给出的线路参数为实际值。系统两侧的电源设置开始为交流50Hz电压源,40 ms后系统发生振荡,振荡参数为:两侧电源相位第一次相差180°的时间为0.8s,两侧电源频率最大差值为10 Hz,从第一次相差180°到达最大频率差的时间为2.2s。
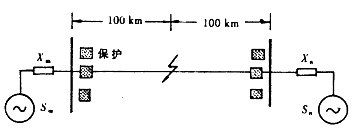
图1 系统接线图
线路每km长参数:
R0=0.26 R1=0.027
X1m=23.0 L0=0.733 L1=0.277 X0m=3.0
X0m=30.0 C0=0.00859 C1=0.013 X1m=23.0
图2为通过仿真由F2250测试仪输出所给出的两端电源系统发生纯振荡时电流、电压模拟波形。

图2 F2250输出的纯振荡仿真波形
图3为F2250测试仪输出在系统发生振荡600 ms后线路中点出现三相短路电流、电压模拟波形。

图3 F2250输出的振荡中三相短路仿真波形
3 结束语
通过建立振荡时电源频率变化数学模型,定义了振荡时电源频率变化函数,解决了EMTP程序不能直接使用可变频率电源的问题。用EMTP程序仿真计算出系统在各种振荡方式和振荡过程中发生故障时保护安装处电流、电压的暂态数据,并将暂态数据通过F2250测试仪变为模拟量波形输出,为研究继电保护装置在系统发生振荡情况下及振荡中又有故障时的动作特性提供了一种有效手段。
|


