|
摘 要 输电线路的重合闸时刻对于重合闸完成后系统的稳定性有明显的影响。即使是重合于永久性故障,只要在最佳时刻重合闸同样可以显著改善系统的稳定性。线路的最佳重合时刻随系统的运行方式而改变,为了在线计算线路故障后的最佳重合时刻,文中将EEAC理论用于最佳重合时刻的计算。对实际系统的仿真表明,用EEAC等值实时计算最佳重合时刻是可行的。
关键词 电力系统 重合闸 系统稳定 EEAC
分类号 TM 712
0 引言
采用自动重合闸可以提高系统安全供电和稳定运行的可靠程度,但是重合于永久性故障对系统可能造成的危害仍不容忽视。为减小或避免重合于永久性故障对系统的危害,提出了自适应重合闸[1],其实质是正确识别瞬时与永久故障,然后作出是否重合的决策。
在目前的实际系统中,正确区分瞬时与永久故障还存在困难,所以考虑到在一定时间重合到永久性故障对系统稳定的不利影响而限制一些线路的输送功率。文献[2]通过对单机无穷大系统的分析指出,在最佳时刻重合于永久性故障,不但不会引起系统失稳,反而会阻尼系统的振荡。而对于在故障后回摆中失稳的系统,在最佳时刻重合于永久性故障还可能保持系统稳定。文献[3]分析了系统在回摆中失稳的条件。文献[4]用多机系统的能量函数分析了不同时刻重合于永久性故障对系统稳定性的影响。本文给出了一种利用EEAC等值来快速计算永久性故障最佳重合时刻的方法。对实际系统的仿真表明,用EEAC等值实时计算最佳重合时刻是可行的,计算速度非常快。
1 基于EEAC的计算方法
根据文献[4]中的结论,永久性故障的最佳重合时刻满足的条件是,重合不成功故障再次切除后系统的暂态能量最小。研究表明,系统的稳定性主要决定于临界机的暂态能量,所以EEAC[5,6](Extended Equal-Area Criterion)将多机系统分解成两个子集,并将两个子集分别在它们各自的部分角度中心(PCOA)坐标系中变换成等值的两机系统,并进一步将这两机系统变换成一个单机无穷大系统,然后用等面积准则(EAC)进行稳定性分析[5]。本文将EEAC理论用于计算给定输电线路在永久性故障下的最佳重合时刻,使得最佳重合时刻满足重合不成功故障再次切除后等值系统的暂态能量最小,也即使得临界机的暂态能量最小。
EEAC将系统的所有发电机分为两群,临界群和其余机群,设:S为临界机群的集合;s为S集的等值单机;A为所有其余机组的集合;a为A集的等值单机。
可以得到多机系统用EEAC等值后如式(1),等值的方法参见文献[5]。
M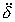 =Pm-[Pc+Pmax sin(δ-υ)](1) =Pm-[Pc+Pmax sin(δ-υ)](1)
当用EEAC法求取临界切除时间(CCT)时,临界失稳机的选取直接关系到计算的精度。实际电力系统地域分布很广,在某一地点发生的故障,对全系统中所有发电机的影响是不相同的。一般,CCT只与最先失稳的发电机(组)有关,这样的发电机数目相对来说是很少的,困难就在于如何从所有发电机中正确地选出临界失稳的机组。而对于以计算最佳重合闸为目的的EEAC等值,机群的划分要相对容易一些,因为这里的主要目的是在系统实际的故障切除条件下将系统分群,而不是求故障的临界切除时间,所以通过选择系统最严重的故障形式,利用文献[3]所述的方法将系统分为两群。将文献[3]的方法用于本文时的主要思想为,在感兴趣的最严重条件下求取系统的受扰轨迹,在最大可能的最佳重合时刻(一般为2 s)前根据系统发电机之间的位置间隙将所有发电机分群。
对于给定线路,用以上思想将系统分为两群,然后用EEAC等值,令故障期间的等值系统方程为:
M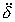 =Pm-[Pc′+Pmax′ sin(δ-υ′)](2) =Pm-[Pc′+Pmax′ sin(δ-υ′)](2)
第1次故障切除后等值系统的运动方程为:
M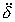 =Pm-[Pc″+Pmax″ sin(δ-υ″)](3) =Pm-[Pc″+Pmax″ sin(δ-υ″)](3)
重合不成功故障线路切除后的等值系统运动方程为:
M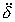 =Pm-[Pc+Pmax sin(δ-υ)](4) =Pm-[Pc+Pmax sin(δ-υ)](4)
与式(4)对应的系统能量函数方程为:
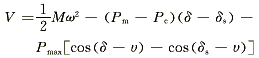 (5) (5)
当故障类型为多相故障时式(3)和式(4)是相同的。
用EEAC计算永久性故障最佳重合时刻的步骤为:
a.对给定线路以及故障,将系统分为两群;
b.由分群得到等值系统的方程式(2)~式(4)以及能量函数方程式(5);
c.以故障前的系统状态变量作为初值,用数值积分求解式(2),直至首次故障切除;
d.用首次故障切除时刻系统的状态变量作为初值,用数值积分求解式(3),输出第1次故障后重合前各个时刻等值系统的状态变量δ(t)和ω(t),一般只需要计算1.5 s就可以;
e.用步骤d计算出的各个时刻的δ(t)和ω(t)依次作为初值,用数值积分求解式(2),积分的时间长度为第2次故障的持续时间,输出第2次切除故障线路时系统的状态变量δ(t+Δt)和ω(t+Δt),一般只需用步骤d结果的0.5 s以后的值开始计算即可;
f.用步骤e的计算结果δ(t+Δt)和ω(t+Δt)来计算式(5)所对应的暂态能量,此能量是随时间变化的;
g.由步骤f计算出的暂态能量的最小值所对应的时刻t就是永久性故障的最佳重合时刻。
对于以上的计算过程,费时较多的是步骤a和步骤b,但这两步的计算可以在没有故障的情况下完成,故障后只需要从步骤c开始计算。另外,由于一般情况下1.5 s以后系统的回摆过程已经结束,所以步骤d中只需要计算1.5 s。又因为一般情况下0.5 s以后发电机的回摆过程刚开始,所以步骤e中只需从0.5 s开始对式(2)计算就可以了。仿真表明,除去步骤a和步骤b,其余过程的计算只需要十几毫秒。
2 仿真
算例为西北电力系统,其主要接线形式和故障地点如图1所示,故障类型为三相故障,下面用EEAC等值来计算永久性故障的最佳重合时刻。

图1 西北电网主要接线图
Fig.1 The main structure
of Northwest Power System
对以上线路,根据故障条件的分群结果为:关中电网的机组(包括安康电厂)为一群,另一群为西部电网的机组。通过机群划分可容易地求得等值单机无穷大系统的参数。等值后的系统参数如表1所示。故障前等值系统初值为:δ0=-13.22°,ω0=0。
表1 等值系统的参数
Table 1 The parameters of the reduced system
等值系统
M
Pm
Pc′(Pc″)
Pmax′
(Pmax″)
υ′(υ″)
故障线路切除后
0.697
0.094
-1.197
7.466
8.593
故障期间
0.697
0.094
-12.086
3.420
6.984
等值系统的暂态能量函数方程可以较容易地由以上参数得到。
根据第1节给出的步骤计算出各个时刻重合于永久性故障再次切除后系统的暂态能量,如图2。可见等值系统的最佳重合时刻为1.2 s。图3是两种重合时刻下等值系统的摇摆曲线。图3表明,在最佳时刻重合于永久性故障可以很好地阻尼系统的振荡。
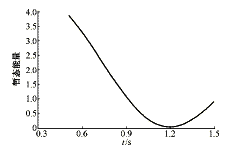
图2 计算最佳重合时刻的能量曲线
Fig.2 Energy curve
to obtain the optimal reclosing time
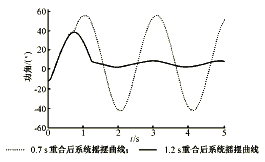
图3 不同时刻重合后等值系统的摇摆曲线
Fig.3 Generator angle curve
at different reclosing time
为了验证用EEAC计算出的最佳重合时刻应用于实际系统的效果,下面给出对实际系统的仿真,仿真中采用的是系统的复杂模型。
图4为实际系统在0.1 s切除故障,各种重合时刻下系统中关中电网某主要机组与西部电网某主要机组之间功角的振荡情况。图5为各种重合时刻下安康电厂机组与西部电网某主要机组之间功角的振荡情况。
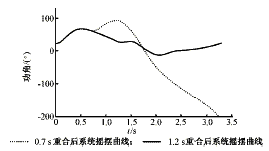
图4 两个主网之间功角曲线
Fig.4 Generator angle curve
between two systems
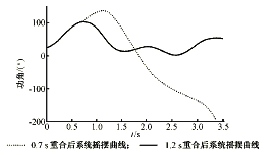
图5 安康厂与西部网的功角曲线
Fig.5 Generator angle curve between Ankang
generator and West Power System
图4和图5的计算结果表明,0.7 s重合于永久性故障不成功,再次跳开后系统在回摆中失稳,而1.2 s重合于永久性故障,再次切除后系统稳定。
鉴于目前在实际系统中还不能够正确区分瞬时与永久故障,所以按照永久性故障的最佳时刻来计算重合闸时刻对于系统稳定是有利的。
3 结语
在目前的实际系统中,正确区分瞬时与永久性故障还存在困难,所以考虑到在一定时间重合到永久性故障对系统稳定不利的影响而限制一些线路的输送功率,为此研究重合于永久性故障对系统稳定的影响,计算永久性故障的最佳重合时刻具有实际的意义。本文给出了一种利用EEAC等值来快速计算永久性故障最佳重合时刻的实用算法。对于实际系统的仿真表明,利用EEAC计算最佳重合时刻是可行的。
资助项目:国家自然科学基金资助项目(59677012)。
作者简介:袁宇春,男,1970年生,博士,现在浙江大学和北海银河公司博士后工作站工作,研究方向为电力系统稳定分析及控制、配网自动化。
张保会,男,1953年生,博士,教授,博士生导师,研究方向为电力系统稳定分析及控制、电力系统继电保护。
作者单位:袁宇春(浙江大学电机系 310027 杭州)
张保会(西安交通大学电力工程系 710049 西安)
参考文献
1 Ge Yaozhong, Sui Fonghai, Xiao Yuan. Prediction Method for Preventing Single-Phase Reclosing on Permanent Fault. IEEE Trans on Power Delivery, 1989, 4(1)
2 王梅义,吴竞昌,蒙定中.大电网系统技术.北京:中国电力出版社,1995
3 薛禹胜.非自治非线性多刚体系统运动稳定性的定量分析.电力系统自动化,1998,22(1)~1998,22(12)
4 袁宇春,张保会,阎海山.多机电力系统中重合闸最佳时刻的研究:第2部分 永久性故障最佳重合时刻的研究.电力系统自动化,1998,22(6)
5 电力部电力自动化研究院.电力系统安全稳定分析的新算法——关于EEAC算法的论文集(二). 南京:1994
6 Xue Y, Van Cutsem Th, Ribbens-Pavella M. A Simple Direct Method for Fast Transient Stability Assessment of Large Power Systems. IEEE Trans on Power Systems, 1988, 3(2):400~412
|


