1　引言
　　大量非线性负载在电力系统中的应用带来了日益严重的谐波污染，消除谐波的危害越来越受到人们的重视。瞬时无功功率理论^［1］的提出使有源滤波器在电力系统中得到了广泛应用。为了更加准确地、实时地检测出电网中瞬态变化的谐波，人们提出了基于傅立叶级数的实时检测法^［2］、基于Fryze时域分析的有功电流分离法^［3］，以及基于自适应干扰抵消原理的自适应闭环检测法^［4］等。
　　文［2］所述方法能较好地分离出基波有功电流，但该方案的实现需多次使用带通滤波器，滤波器的中心频率对元件参数十分敏感，当电网频率发生波动时，不仅影响检测精度，而且检测出的谐波电流中还含较多的基波分量，大大地增加了有源滤波器的容量和运行损耗。文［3］所述方法的主要缺点是要计算出有功电流，必须对上1个周期的电流、电压进行积分运算，因此该方法检测出的广义无功电流瞬时值至少有1个周期以上的时间延迟。文［4］所述方法具有良好的自适应能力，检测精度较高，但该方法实现起来较为复杂。
　　本文讨论的基于dq理论的谐波检测方案适用于三相三线制电力系统，对该方案的检测性能用SABER软件做了灵敏度分析和Monte－Carlo分析，详细讨论了dq检测电路中各主要部件的参数对谐波检测性能的影响。分析表明，传统的dq检测方案的检测精度受部件参数波动的影响较大。为了降低谐波检测结果对主要部件参数的灵敏度，本文提出了一种改进型的谐波检测方案。该方案的优点是

    ·降低了主要部件参数对谐波检测精度的影响；

    ·形成闭环反馈系统，保证了检测精度；
    ·降低了实际谐波检测电路的成本。
2　基于dq变换的谐波检测方法

    与文[1]提出的瞬时无功功率理论相比，基于dq变换的谐波检测方法的优点在于可以消除电压谐波和不对称电压的影响，而且将基波分量在dq坐标中变换到零频率处，用Butterworth低通滤波器提取基波信号可以消除模拟滤波器的相位问题，且不会造成对有些频率分量的增大或衰减。
　　图1为用dq变换计算谐波的框图。三相电压（电流）信号经αβ（3相－2相）变换及dq变换后，基波有功分量转化为直流信号。用低通滤波器将其与谐波分量和基波无功分量分离，然后经dq反变换及αβ反变换（2相－3相）使基波有功分量还原，最后与输入信号相减得到谐波分量和基波无功分量之和。
                               　　

             
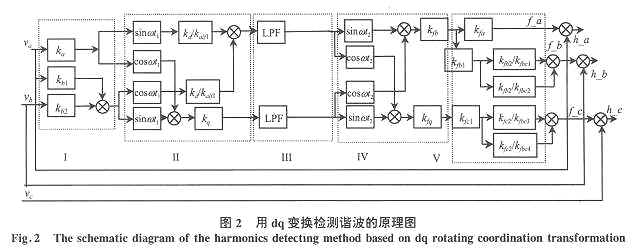
    图2为用dq变换计算谐波的原理图。其中部分Ⅰ、Ⅱ分别实现αβ及dq变换，即

部分Ⅳ为输入与输出信号相减。图2中各部件主要参数的标准值及其变化范围列于表1。

3　灵敏度分析
　　对上述谐波检测方案作参数灵敏度分析，以检测出来的三相基波（f_a、f_b、f_c）的峰值作为检测的性能指标，则参数灵敏度的表达式为

                          
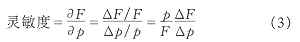
式中　p为波动参数的标准值；Δp为参数的波动量；F为检测出的基波峰值的标准值；Δp为基波峰
值随参数波动的变化量。
　　表1中各参数的灵敏度分析结果如图3中空心棒所示。
　　图3中灵敏度为正值，说明当某一参数增加时，检测出的基波的峰值增加；反之，基波的峰值减少。为使检测精度达到1％，要求主要部件参数的灵敏度小于1％，而从图3可见，主要部件的参数对三相基波峰值的灵敏度均大于1％。尤为重要的是，该系统对标准正、余弦幅度的依赖性很强，对它们的精度要求很高，而在实际电路中作到这一点是很困难的。
  

　　为了降低系统对参数的依赖性，本文对上述方案做了改进。即在低通滤波器之后加入PI调节器，形成1个闭环系统。其原理如图4所示，主要参数与表1相同。
                    　　
　　此闭环检测方案的参数灵敏度分析结果如图3中实心棒所示。由图可见，灵敏度大于1％的参数的数目大量减少，并且与方案1相比较，各参数灵敏度的绝对值也有所降低，亦即输出基波峰值的波动范围有所减少。从图3还可以看到，标准正、余弦幅度的灵敏度明显降低。从式（1）可推出

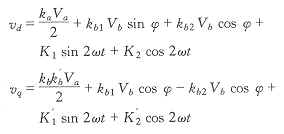
　　可见，经过dq变换后得到的信号是直流信号与交流信号之和，经低通滤波器滤波后送到PI调节器
的信号主要是直流，经过积分再送到dq反变换部分，因此PI调节器之前环节的参数灵敏度得以降低。
4　MONTE－CARLO分析
　　Monte－Carlo分析是在已知电路元器件参数的统计规律基础上，根据这些统计分布规律随机多次抽样元器件参数，并且对随机抽样所得的电路进行计算机模拟，从而估计出电路性能的统计分布规律。

    为了进一步比较上述2种谐波检测方案的精度，分别对它们进行了Monte－Carlo分析。分析时设各参数的统计分布规律为正态分布，检测精度为5％。图5为传统检测方案的Monte－Carlo分析结果，图6为改进型检测方案的Monte－Carlo分析结果。图中ERR_max为检测出的基波（f_a、f_b、f_c）与三相输入基波含量（f_ain、f_bin、f_cin）的最大值误差。从图中可见，传统检测方法的a相最大值误差主要集中在±0．2V之间，其误差百分比为4％，而相应的改进型检测方案的误差集中在0．03～0．05V之间，误差百分比为0．4％。同理可得b、c相的误差分析，列于表2。其中c相误差较大，主要原因是c相在改进型检测方法中处于不控状态。尽管如此，改进型检测方法的误差显著比传统方法的少，保证了检测精度。　　

5　改进型谐波检测方案用于串联型混合有源滤波器的仿真结果及实验结果　　
　　将本文提出的改进型检测方法应用于一串联型混合有源滤波器，其补偿对象是35 k W的变频器，负载的变化率为每十几个周期改变1％，因此PI调节器带来的时间延迟可以忽略不计。图7（a）为用传统的检测方案进行补偿的结果，图7（b）为用改进检测方案进行补偿的结果。比较图7（a）、（b），采用改进型谐波检测方案，补偿后线电流中谐波含量与基波含量之比为3％，而用传统方案进行谐波提取，补偿后线电流中谐波含量与基波含量之比为7％，未达到国家标准（5％）。实验结果如图8所示，图中波形由上至下分别为含谐波的电网电流波形、dq变换提取出的电网基波电流波形和电网电流中的谐波。

6　结论

　　本文提出的基于dq变换的改进型谐波检测方案，有效地降低了检测系统中各主要参数对系统的灵敏度，保证了检测精度，从系统仿真结果及实验结果可见，它比传统方法有较大的改进。