|

半导体的激光微细加工技术具有“直接写入”、“低温处理”等独特的优越性,在微电子、光电子、集成光学及光电混合集成等领域有着广阔的应用。如制作OEIC(光电混合集成)器件时,可以把电路和光路部分分开来做,即先在半导体衬底上做好集成电路,再利用激光微细加工的直接写入功能,一次性“写入”p-n结和欧姆接触,可以避免高温热损坏半导体基片和集成电路,从而可以使OEIC各个部分性能达到最优,大大提高OEIC的整体性能。因此,自20世纪70年代末期以来,国内外在这方面的研究都比较活跃。
在激光微细加工技术中,人们需要了解曝光区温度分布的细节,尤其是焦斑中心温度、热斑边界等重要信息。针对半导体基片温度的测量方法已有很多报道,但大多是测量基片的平均温度,不能满足上述要求。本课题组曾经报道的微小高温区温度不接触实时测量系统,测量区域直径最小可以达到18μm,温度分辨能力可以达到1℃,基本满足激光微细加工的要求。但系统在实际应用时遇到几个问题。首先是要进一步提高温度分辨率时,测温范围达不到要求。其次是测量曝光区温度分布时,需手动调节测温套筒的位置,系统的调整和读数不方便,只能测较少的点,不能很好的反映曝光区的温度分布,同时难以寻找到曝光区的最高温度点,使得测温带来误差。本文首先简单介绍现有系统的结构和工作原理,然后详细分析了产生这些问题的原因,以及对温度测量的影响。在此基础上,提出一种计算机温度测量系统,较好的解决了这些问题。该系统采用高精度、低漂移电流放大器对光电探测器产生的光电流进行放大,并将放大后的电压信号转换为数字信号输入计算机进行记录、处理,在温度为600℃附近,将温度分辨率提高到0.2℃,并且扩大了测温范围。通过计算机软件对最高光电流值进行判断,可精确调整测温套筒,使半导体基片表面位置位于探测器光敏面的共轭面位置。同时,计算机通过对曝光区进行快速扫描,获得温度场的分布,以及对最高温度点进行准确定位。
1.系统实验装置和工作原理
系统实验装置如图1所示,CO2激光器输出的10.6μm激光束经反射镜M、锗透镜L2聚焦后照射在表面已制备好含Zn的SiO2乳胶膜的半导体基片S上,完成扩散结的写入等。曝光区近似为圆。基片上曝光区受激光照射升温而发出较强的热辐射,由透镜L1将曝光区中被测面元的热辐射能会聚在探测器D的光敏面上,并通过光电探测器把被测面元的热辐射转换为光电流,实际上也就是把被测面元的温度信号变为电流信号,最后通过检流计显示出光电流值,据此可得出相应的温度值。
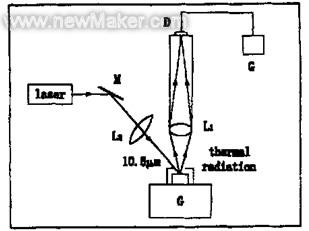
图1 温度测量系统的实验装置
合理地将曝光区Σ近似为灰体,其面发光率
R=KσT4(1)
式中,K是被测基片在Σ区的平均发射本领,σ为Stefan常数,T为曝光区中测量点的温度。进一步假设透镜接受到的被测面元(探测器光敏面的共轭面元)的辐射全部会聚到探测器光敏面,则探测器D输出的光电流为
IP=RI(T)KσT4S1S′/(πd21)(2)
式中,RI(T)为探测器的电流响应率,S1为透镜L1的通光孔面积,S′为测量区域面积,即Σ中与探测器D的光敏面共轭面元的面积,d1为L1到基片表面的距离。
(2)式表明,探测器D输出的光电流对温度的变化非常敏感,只要对光电流有一定的分辨率,就可达到较高的温度分辨率。显然,这种辐射测温法具有不接触测量的功能。
由于探测器光敏面的共轭面元(被测面元)面积S′、发射本领K难以准确测定,电流响应率RI(T)是温度函数,所以依据式(2)用理论计算的方法由光电流IP求出温度T比较困难。实验中,需进行温度定标,即确定检流计的电流示值同被测面元温度之间的关系。温度定标的实验方法见文献[6],通过温度定标后,就可以根据检流计的电流示值读出温度值。
2.系统在实际使用时遇到的问题
2.1温度分辨率和测量范围不能同时满足要求
图2 是系统对GaAs基片进行定标实验的结果。从图中可以看出,当温度从400℃变到700℃时,光电流将从几个纳安变到一百多个纳安,变化范围很大。系统中采用检流计来测量探测器产生的光电流。当采用检流计的高灵敏度档时,量程不能满足这样宽的测量范围。因此只能使用检流计的次灵敏档,但这样测量得出的精度又不能令人满意。由于光电流与温度的非线性关系,特别是在低温时,光电流分辨率的降低使得温度分辨率很低。这一点从图2中可以看出。在温度为600℃时,光电流分辨率为InA对应的温度分辨率约为1℃,而在温度为450℃时,对应的温度分辨率降为约10℃。因此,需要采用新方法在不减小测量范围的条件下提高对温度的分辨率。
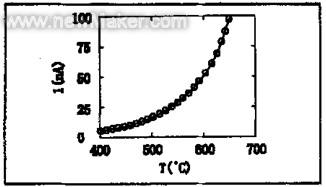
图2 定标实验结果
2.2不能准确测得温度场的分布及对曝光区最高温度区域进行定位
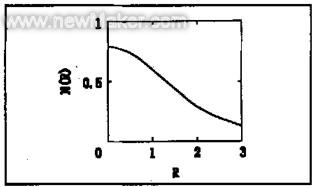
图3 温度的径向分布曲线
合理假设加热基片的聚焦激光束为高斯光束,在基片表面光强分布为高斯分布,光斑半径为w,则基片表面曝光区Σ的温度场的径向分布为
T(R,W)=TmaxN(R,W)
式中,R=r/w是离束斑中心的径向距离(以光斑半径作为单位),W=αw,α为吸收系数,Tmax是吸收系数很大时(W→∞),基片表面光斑中心的温度。归一化温度场径向分布函数为
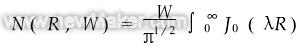 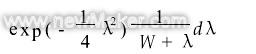 (3) (3)
取α=1/20μm,W=24μm,得W=1.2。据式(3)做出的N(R)~R关系曲线如图3所示。
由图3可看出,曝光区内的温度分布是不均匀的,具有较大的温度梯度。在进行激光微细加工实验时,需要测出温度场的分布。另外,实验需用最高温度区域的温度来表示加工温度。因此,需调节套筒位置,使得测量区域为最高温度区域。可以通过移动测温套筒,逐点记录温度值及对应的套筒坐标的方法来测量温度场的分布和寻找最高温度区域。但由于调节台的坐标值和检流计的电流示值要用人工方法记录成表格,测量一个点的时间较长。同时必须要测量尽量多的点才能真实反应温度场的分布。这样,即使进行一维的测量,也要花费很长时间。重要的是,要这样一段长的时间里,由入射激光功率本身的变化,整个温度场的温度都会做相应的变化,这事实上使得用这种方法测量温度场变得无法实现。而最高温度点需要在整个曝光区寻找,应在得到温度场分后才能准确获得。因此,必须另寻方法来测量温度场的分布。
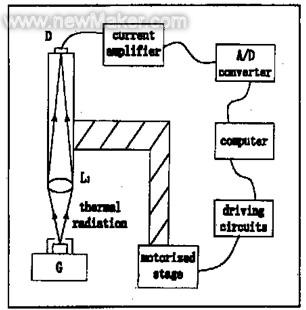
图4 计算机温度测量系统实验装置
3.系统的改进
针对系统在实际使用时遇到的困难,我们对原系统进行了改进。改进后测温系统的装置如图4所示。系统去掉了检流计,采用高精度电流放大器将探测器产生的光电流信号转换为电压信号,再经A/D转换器转为数字信号输入计算机进行计算、记录及显示。通过实验定标,可将数字量直接和温度对应。这样,不但解决了测量范围与测量精度之间的矛盾,还使得实验时读数方便、准确。温度分辨率主要决定于所选A/D转换器的位数,并不影响测量范围。实验装置中,采用集成运放OP37组成电流放大器,A/D转换器选用AD1674A。在温度为600℃时,温度分辨率达到0.2℃。
计算机控制精密电动平台带动测温套筒移动并同时记录由探测器输出的温度信号,对基片上的热斑作二维扫描得到热斑的温度分布,从而利用软件测出焦斑中心温度、热斑边界等参数。同时,利用计算机软件计算出热斑最高温度区的位置,并使测温套筒移动,对准该位置。精密电动平台的步距为1.25μm,扫描速度达20mm/s,满足我们对温度分布测量的要求。
在测量之前,同样需对系统进行定标。在得到定标数据后,利用计算机的快速计算,在对实验中的基片进行温度测量时,将从A/D转换器读出的数据字量用插值计算的方法直接转换为温度值显示在我们设计的虚拟仪器面板上。这很大程度上方便了激光微细加工实验中对温度的调节。
另外,我们利用计算机软件及系统对温度信号的快速记录功能,实现了对基片温度随时间变化过程的测量、记录。
4.改进后的系统在实验中的应用
我们用上述系统测量了用功率为10W的连续波10.6μm聚焦激光束照射预热温度为580K的InP时产生热斑的温度分布,电动平台移动的速度设置为0.5mm/s,结果示于图5。从图中可以看出,热斑随半径有较大的温度梯度。热斑中心温度随时间变化过程如图6所示。
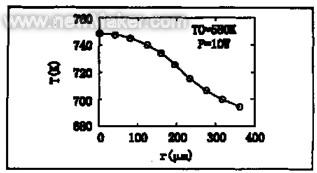
图5 热斑的温度分布
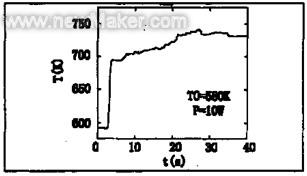
图6 热斑中心温度随激光束照射时间的变化
5.结束语
现有用于半导体的激光微细加工中微小曝光区的温度测量系统在实际使用过程中出现了一些需要解决的问题。首先是温度分辨率和温度测量范围不能同时满足使用要求,其次是不能进行温度分布的准确测量和最高温度点的准确定位。本文提出了一种在原有系统基础上经过改进的计算机温度测量系统,该系统通过软、硬件的结合,较好的解决了原有系统的这些问题。新的计算机温度测量系统在半导体的多种激光微细加工实验中将发挥重要作用。
参考文献
[1]叶玉堂.激光微细加工.第一版.电子科技大学出版社,1995
[2]叶玉堂、李忠东等.GaAs衬底的固态杂质源脉冲1.06μm激光诱导扩散.光学学报,1997,17(4)
[3]叶玉堂、李忠东等.用固态杂质源在GaAs衬底上实现的连续波CO2激光诱导Zn扩散.中国激光,1997,24(3)
[4]P.Baumgartner, W.Wegscheider, M.Bichier, etal. Single-electron fabricated by focused laser beam-induceddoping of a GaAs/AlGaAshetero structure, Appl. Phys. Lett,1997,70(16)
[5]A.Yu.Bonchik,S.G.Kijak,Z.Gotra,etal.Laser technology for submicron-dopedlayers for mation in semiconductors, Optics & Laser Technology, 2001
[6]李忠东、叶玉堂.连续波激光诱导扩散区温度的不接触测量.应用科学学报,1997,15(4)
|


